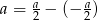/Szkoła średnia/Zadania z treścią

Zadanie nr 8894411

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczbę a przedstaw w postaci różnicy dwóch liczb tak, aby suma kwadratów tych liczb była najmniejsza.

Rozwiązanie

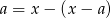Niech te liczby będą równe x i a− x (czyli a = x − (x − a) ). Suma kwadratów tych liczb jest równa

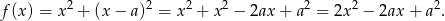
f(x) = x 2 + (x − a )2 = x2 + x2 − 2ax + a2 = 2x 2 − 2ax + a2.

Wykresem tej funkcji jest parabola o ramionach skierowanych do góry i wierzchołku w punkcie

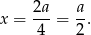
2a a x = ---= --. 4 2

Zatem najmniejszą sumę kwadratów otrzymamy dla 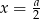a x = 2 .  
Odpowiedź: a a a = 2 − (− 2)

Wersja PDF