Zadanie nr 9220466
Ewa jadąc drogą widziała elektrownię wiatrową oznaczoną na rysunku literą 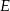 . Z punktu
. Z punktu 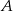 widziała ją pod kątem
widziała ją pod kątem 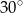 stopni do kierunku drogi. A z punktu
stopni do kierunku drogi. A z punktu 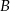 pod kątem
pod kątem 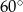 . Przejeżdżając przez punkt
. Przejeżdżając przez punkt 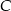 minęła elektrownię. Długość odcinka
minęła elektrownię. Długość odcinka 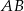 jest równa 20km.
jest równa 20km.
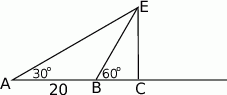
- Oblicz miary kątów
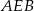 i
i 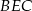 .
. - Oblicz długość odcinka
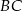 .
. - Oblicz odległość elektrowni od drogi.
W rachunkach przyjmij, że 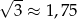 .
.
Rozwiązanie
- Ponieważ
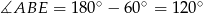 , mamy
, mamy 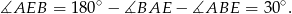
Ponadto patrząc na trójkąt
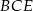 mamy
mamy 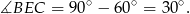
Odpowiedź: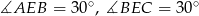
- Jak zauważyliśmy wyżej, trójkąt
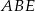 jest równoramienny, czyli
jest równoramienny, czyli 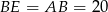 . Ponadto
. Ponadto 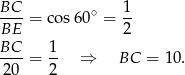
Odpowiedź: 10km -
Sposób I
Liczymy
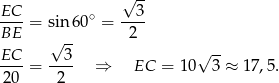
Sposób II
Skoro wiemy, że trójkąt
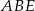 jest równoramienny i
jest równoramienny i 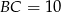 , możemy długość
, możemy długość 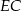 wyliczyć z twierdzenia Pitagorasa.
wyliczyć z twierdzenia Pitagorasa. 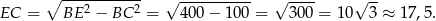
Odpowiedź: 17,5km

