/Szkoła średnia/Zadania z treścią

Zadanie nr 9299306

Dodaj do ulubionych
Dodaj do rozwiązanych

Grupa znajomych wyjeżdżających na biwak wynajęła bus. Koszt wynajęcia busa jest równy 960 złotych i tę kwotę rozłożono po równo pomiędzy uczestników wyjazdu. Do grupy wyjeżdżających dołączyło w ostatniej chwili dwóch znajomych. Wtedy koszt wyjazdu przypadający na jednego uczestnika zmniejszył się o 16 złotych. Oblicz, ile osób wyjechało na biwak.

Rozwiązanie

Sposób I

Jeżeli oznaczymy liczbę znajomych przez n , a oryginalny koszt wynajęcia busa przypadający na jedną osobę przez x , to mamy układ równań

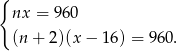
{ nx = 96 0 (n + 2)(x− 16) = 960 .

Przekształćmy drugie równanie

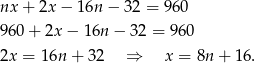
nx + 2x − 16n − 3 2 = 960 9 60+ 2x − 16n − 32 = 960 2x = 16n + 3 2 ⇒ x = 8n + 16.

Podstawiamy to wyrażenie do równości 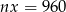nx = 960 i mamy

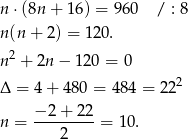
n ⋅(8n + 16 ) = 960 / : 8 n(n + 2 ) = 120. n2 + 2n − 1 20 = 0 2 Δ = 4+ 480 = 4 84 = 22 −-2+--22- n = 2 = 10 .

Na wycieczkę pojechały o 2 osoby więcej.

Sposób II

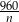Jeżeli oznaczmy liczbę znajomych przez n , to początkowo każdy z nich miał zapłacić 960 n . Po dołączeniu 2 znajomych koszt ten zmalał do 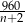-960 n+ 2 . Z drugiej strony wiemy, że wysokość składki zmalała o 16 zł. Mamy więc równanie

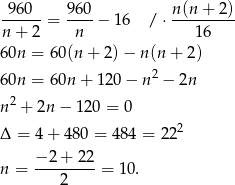
960 960 n (n+ 2) ------= ----− 1 6 / ⋅--------- n + 2 n 1 6 60n = 60(n + 2) − n(n + 2 ) 2 60n = 60n + 120 − n − 2n n2 + 2n − 120 = 0 Δ = 4+ 480 = 484 = 222 −2 + 2 2 n = ---------= 10. 2

Na wycieczkę pojechały o 2 osoby więcej.  
Odpowiedź: 12 osób

Wersja PDF