/Szkoła średnia/Zadania z treścią

Zadanie nr 9455554

Klasa IIIb liczy o jednego ucznia więcej niż klasa IIIa. Na koniec roku okazało się, że suma ocen z matematyki uzyskanych przez uczniów klasy IIIa jest równa 97,5 i jest jednocześnie równa sumie ocen z matematyki uzyskanych przez uczniów klasy IIIb. Gdy obliczono średnie z tych ocen w każdej z klas to okazało się, że średnia w klasie IIIa była wyższa o 0,15 niż średnia uzyskana w klasie IIIb. Oblicz ilu uczniów liczą obie klasy.

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy średnią ocen w klasie IIIa przez s , a liczbę uczniów tej klasy przez n to to mamy układ równań

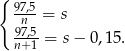
{ 97,5 -n--= s 97,5= s− 0,15. n+ 1

Podstawiamy 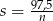97,5- s = n z pierwszego równania do drugiego.

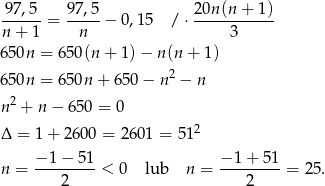
9 7,5 97,5 20n (n + 1) ------= -----− 0,1 5 / ⋅----------- n + 1 n 3 650n = 650(n + 1) − n(n + 1) 2 650n = 650n + 65 0− n − n n2 + n − 650 = 0 2 Δ = 1+ 2 600 = 26 01 = 51 − 1 − 51 − 1+ 51 n = ---------< 0 lub n = ---------= 25 . 2 2

Ujemne rozwiązanie odrzucamy i mamy 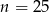n = 25 . W takim razie w klasie IIIb uczyło się 26 uczniów.  
Odpowiedź: 25 i 26

Wersja PDF