/Szkoła średnia/Zadania z treścią

Zadanie nr 9624148

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwa miasta łączy droga o długości 448 kilometrów. Samochód 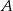A przebył tę trasę w czasie o 40 minut krótszym niż samochód 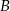B . Średnia prędkość samochodu 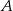A na tej trasie była o 12 km/h większa od średniej prędkości samochodu 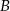B . Oblicz średnią prędkość każdego z tych samochodów na tej trasie.

Rozwiązanie

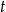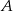Niech t i v oznaczają odpowiednio czas przejazdu oraz prędkość samochodu A . Z założeń mamy

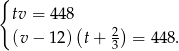
{ tv = 448 (v − 12 )(t+ 2) = 44 8. 3

Podstawiamy 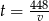448- t = v z pierwszego równania do drugiego.

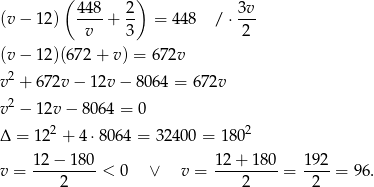
( 448 2) 3v (v − 12 ) ----+ -- = 448 / ⋅--- v 3 2 (v − 12 )(672+ v) = 672v 2 v + 67 2v− 12v − 8064 = 672v v 2 − 12v − 8064 = 0 Δ = 122 + 4 ⋅8064 = 32400 = 1802 12 − 180 12+ 180 192 v = ---------< 0 ∨ v = ---------= ----= 96. 2 2 2

Ujemne rozwiązanie odrzucamy i mamy 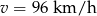v = 96 km/h . Wtedy prędkość drugiego samochodu to

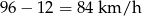
96 − 12 = 84 km/h

 
Odpowiedź: Samochód 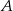A : 96 km/h, samochód 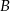B : 84 km/h

Wersja PDF