Zadanie nr 9680884
Z miast 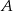 i
i 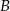 odległych o 330 km wyjechały naprzeciwko siebie dwa samochody. Samochód jadący z miasta
odległych o 330 km wyjechały naprzeciwko siebie dwa samochody. Samochód jadący z miasta 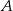 wyjechał 20 minut wcześniej i jechał z prędkością o 9 km/h mniejszą niż samochód jadący z miasta
wyjechał 20 minut wcześniej i jechał z prędkością o 9 km/h mniejszą niż samochód jadący z miasta 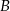 . Samochody te minęły się w odległości 168 km licząc od miasta
. Samochody te minęły się w odległości 168 km licząc od miasta 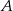 . Oblicz średnią prędkość każdego z samochodów.
. Oblicz średnią prędkość każdego z samochodów.
Rozwiązanie
Oznaczmy szukane średnie prędkości samochodów przez 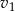 i
i 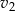 odpowiednio. Do chwili spotkania pierwszy samochód przejechał 168 kilometrów, a drugi
odpowiednio. Do chwili spotkania pierwszy samochód przejechał 168 kilometrów, a drugi 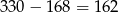 kilometry. To oznacza, że pierwszy jechał przez
kilometry. To oznacza, że pierwszy jechał przez 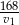 , a drugi przez
, a drugi przez 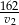 godzin. Wiemy, że pierwszy samochód wyruszył o 20 minut wcześniej niż drugi samochód, co daje nam równanie
godzin. Wiemy, że pierwszy samochód wyruszył o 20 minut wcześniej niż drugi samochód, co daje nam równanie
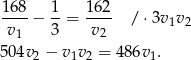
Wiemy ponadto, że 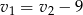 , co po podstawieniu do powyższego równania daje
, co po podstawieniu do powyższego równania daje
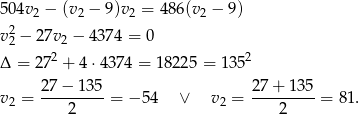
Ujemne rozwiązanie odrzucamy i mamy 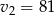 . Stąd
. Stąd 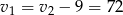 .
.
Odpowiedź: 72 km/h i 81 km/h

