/Szkoła średnia/Zadania z treścią

Zadanie nr 9748673

Dodaj do ulubionych
Dodaj do rozwiązanych

W III wieku p.n.e władca Syrakuz, Hieron II, nakazał złotnikowi wykonać koronę ze sztaby ważącej 8,375 kg. Rzemieślnik wykonał koronę lecz władca podejrzewał, że artysta sprzeniewierzył część otrzymanego kruszcu. Hieron zwrócił się do Archimedesa, aby ten sprawdził, czy złotnik nie zastąpił części złota tańszym srebrem. Sławny fizyk zanurzył koronę w wodzie i sprawdził, że straciła ona pozornie na wadze 0,477 kg. Wiedząc, że złoto traci w wodzie pozornie 0,052 swojego ciężaru, z srebro 0,095, oblicz, ile złota, a ile srebra było w tej koronie. Wynik podaj z dokładnością do 0,001 kg.

Rozwiązanie

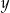Oznaczmy przez x wagę złota, a przez y wagę srebra użytego do wykonania korony. Wówczas z założeń mam

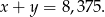
x+ y = 8,37 5.

Zastanówmy się jaki pozorny ciężar mają złoto i srebro zanurzone w wodzie

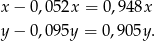
x − 0 ,052x = 0 ,9 48x y − 0 ,0 95y = 0,9 05y.

Korzystając z informacji o pozornej utracie wagi korony otrzymujemy równanie

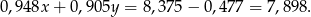
0,948x + 0,90 5y = 8,37 5− 0 ,477 = 7,89 8.

Zatem otrzymujemy układ równań

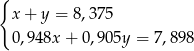
{ x + y = 8,375 0,9 48x + 0,905y = 7,898

Wyznaczamy z pierwszego równania zmienną x

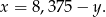
x = 8,37 5− y .

Podstawimy do drugiego równania

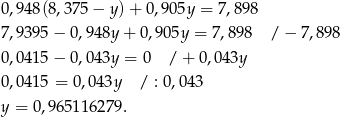
0,948(8,37 5− y)+ 0,905y = 7 ,898 7,9395 − 0,94 8y+ 0,905y = 7,898 / − 7,898 0,0415 − 0,04 3y = 0 /+ 0,043y 0,0415 = 0,043y / : 0,043 y = 0,965 116279.

Stąd

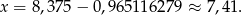
x = 8,375 − 0,965 116279 ≈ 7,41.

 
Odpowiedź: W koronie było 7,41 kg złota i 0,965 kg srebra

Wersja PDF