/Szkoła średnia/Zadania z treścią

Zadanie nr 9786136

Dodaj do ulubionych
Dodaj do rozwiązanych

Koszt godziny pływania pewnego rodzaju łodzi jest sumą kosztu stałego i kosztu zmiennego zależnego od prędkości łodzi. Wiadomo, że koszt stały jest równy 2880 zł/h, a koszt zmienny 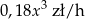0,18x 3 zł/h , gdzie 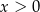x > 0 oznacza prędkość łodzi (w km/h).

  • Przy jakich prędkościach łodzi koszt przepłynięcia 1 km będzie mniejszy niż 306 zł?
  • Przy jakiej prędkości łodzi koszt przepłynięcia 1 km będzie najmniejszy? Oblicz ten koszt.

Rozwiązanie

  • Jeżeli łódź płynie z prędkości 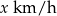x km/h , to jeden kilometr przepływa w 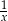1x godziny. W takim razie koszt 1 godziny pracy łodzi to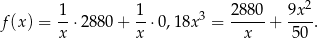
    1 1 3 2 880 9x 2 f(x) = x-⋅2880 + x-⋅0 ,18x = --x-- + -50-.

    Dziedziną tej funkcji jest przedział 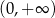(0 ,+ ∞ ) . Pozostało więc rozwiązać nierówność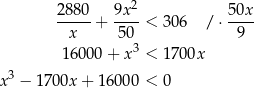

    2880 9x2 5 0x -----+ ----< 3 06 / ⋅---- x 503 9 16000 + x < 1 700x x3 − 1700x + 16000 < 0

    Teraz szukamy pierwiastków wymiernych lewej strony – sprawdzamy dzielniki wyrazu wolnego. Jedynym pierwiastkiem wymiernym jest 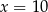x = 10 i mamy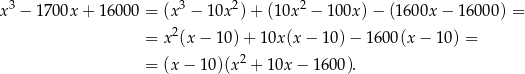

    3 3 2 2 x − 1 700x + 1600 0 = (x − 10x ) + (10x − 1 00x) − (1600x − 16000) = = x2(x − 10) + 10x (x− 10) − 1600(x − 1 0) = = (x − 10)(x2 + 10x − 1600).

    Rozkładamy jeszcze trójmian w nawiasie.

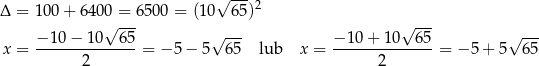
    √ --- Δ = 10 0+ 6 400 = 650 0 = (10 65 )2 √ --- √ --- √ --- √ --- x = −-1-0−-1-0--65 = − 5 − 5 65 lub x = −-10-+-10---65 = − 5 + 5 6 5 2 2

    Mamy więc nierówność

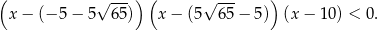
    ( √ ---) ( √ --- ) x− (− 5− 5 65) x − (5 65− 5) (x− 10) < 0.

    Ponieważ interesują nas tylko dodatnie wartości x , rozwiązaniem tej nierówności jest przedział

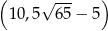
    ( √ --- ) 10 ,5 65− 5

     
    Odpowiedź: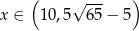 ( √ --- ) x ∈ 10 ,5 65− 5

  • Jak już wiemy z poprzedniego podpunktu, koszt 1 godziny pracy łodzi to
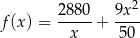
    2 f(x) = 2880-+ 9x-- x 50

    i dziedziną tej funkcji jest przedział 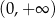(0,+ ∞ ) . Szukamy jej wartości najmniejszej. Liczymy pochodną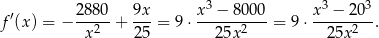

    ′ 2880- 9x- x3 −-8000- x3 −-203- f(x ) = − x2 + 25 = 9⋅ 25x 2 = 9⋅ 2 5x2 .

    Widać teraz, że pochodna jest ujemna dla 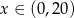x ∈ (0,20) i dodatnia dla 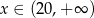x ∈ (20,+ ∞ ) . To oznacza, że funkcja 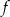f maleje w przedziale 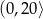(0,20⟩ i rośnie w przedziale 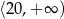⟨20,+ ∞ ) . Najmniejszy koszt pracy statku otrzymamy więc dla prędkości 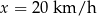x = 20 km/h . Koszt przepłynięcia jednej godziny jest wtedy równy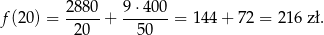

    28 80 9 ⋅400 f (20) = ----- + -------= 144 + 72 = 2 16 z ł. 2 0 50

     
    Odpowiedź: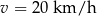 v = 20 km/h , koszt: 216 zł

Wersja PDF