/Szkoła średnia/Zadania z treścią

Zadanie nr 9869893

Dodaj do ulubionych
Dodaj do rozwiązanych

Złotnik ma dwie sztabki wykonane z różnych stopów. Pierwsza sztabka składa się ze 120 g złota i 30 g miedzi, a druga sztabka składa się ze 180 g złota i 20 g miedzi. Ile gramów każdej sztabki powinien wziąć złotnik, aby po stopieniu tych dwóch kawałków otrzymać sztabkę składającą się ze 172 g złota i 28 g miedzi?

Rozwiązanie

Sposób I

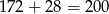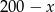Nowa sztabka waży 172 + 28 = 200 gram, więc jeżeli weźmie x gram z pierwszej sztabki, to z drugiej musi wziąć 200 − x gram. Jeden gram pierwszej sztabki zawiera

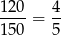
120-= 4- 150 5

gram złota, a 1 gram drugiej zawiera

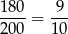
18-0 = -9- 20 0 10

gram złota.

W takim razie w nowym stopie będzie

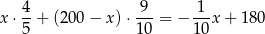
x⋅ 4-+ (200 − x )⋅-9-= − -1-x+ 180 5 10 10

gram złota. Daje nam to równanie

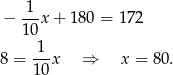
1 − ---x+ 180 = 17 2 10 8 = 1-x ⇒ x = 80. 10

Sposób II

W pierwszej sztabce jest

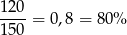
12 0 ---- = 0,8 = 80% 15 0

złota i

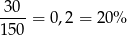
-30- 15 0 = 0,2 = 20%

miedzi. Natomiast w drugiej jest

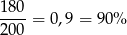
18-0 20 0 = 0,9 = 90%

złota i

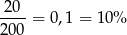
20 ---- = 0,1 = 10% 20 0

miedzi.

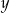Jeżeli oznaczymy ilość potrzebnego stopu z pierwszej sztabki przez x , a ilość stopu z drugiej przez y , to mamy układ równań.

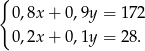
{ 0,8x + 0,9y = 172 0,2x + 0,1y = 28.

Odejmujemy od pierwszego równania drugie pomnożone przez 4 (żeby skrócić x ) i mamy

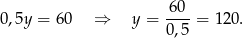
6 0 0,5y = 60 ⇒ y = ----= 120. 0,5

Zatem

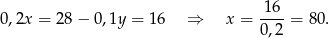
1 6 0 ,2x = 28 − 0,1y = 16 ⇒ x = ----= 80. 0,2

 
Odpowiedź: 80 g i 120 g

Wersja PDF