/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki poziom podstawowy CKE 3 kwietnia 2020 Czas pracy: 170 minut
Zadania zamknięte
Niech 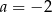 i
i 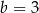 . Wartość wyrażenia
. Wartość wyrażenia 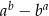 jest równa
jest równa
A) 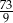 B)
B) 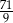 C)
C) 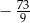 D)
D) 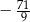
Liczba 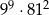 jest równa
jest równa
A) 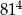 B)
B) 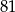 C)
C) 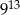 D)
D) 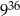
Wartość wyrażenia 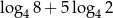 jest równa
jest równa
A) 2 B) 4 C) 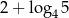 D)
D) 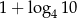
Dane są dwa koła. Promień pierwszego koła jest większy od promienia drugiego koła o 30%. Wynika stąd, że pole pierwszego koła jest większe od pola drugiego koła
A) o mniej niż 50%, ale więcej niż 40%. B) o mniej niż 60% , ale więcej niż 50%.
C) dokładnie o 60%. D) o więcej niż 60%.
Liczba 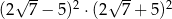 jest równa
jest równa
A) 9 B) 3 C) 2809 D) 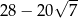
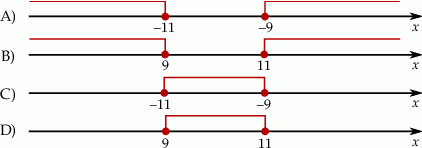
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 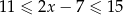 .
.
Rozważmy treść następującego zadania:
Obwód prostokąta o bokach długości  i
i 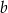 jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 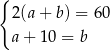 B)
B) 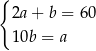 C)
C) 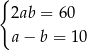 D)
D) 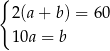
Rozwiązaniem równania 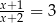 , gdzie
, gdzie 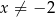 jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 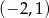 B)
B) 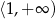 C)
C) 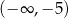 D)
D) 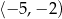
Linę o długości 100 metrów rozcięto na trzy części, których długości pozostają w stosunku 3 : 4 : 5. Stąd wynika, że najdłuższa z tych części ma długość
A) 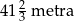 B)
B) 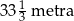 C)
C) 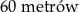 D)
D) 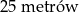
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 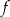 określonej wzorem
określonej wzorem 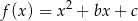 .
.
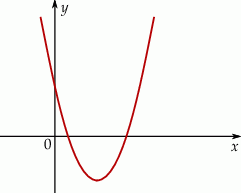
Współczynniki 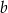 i
i  spełniają warunki:
spełniają warunki:
A) 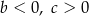 B)
B) 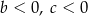 C)
C) 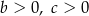 D)
D) 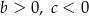
Dany jest ciąg arytmetyczny 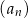 , określony dla
, określony dla 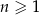 , o którym wiemy, że:
, o którym wiemy, że: 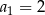 i
i 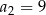 . Wtedy
. Wtedy 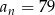 dla
dla
A) 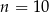 B)
B) 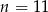 C)
C) 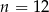 D)
D) 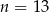
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 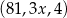 . Stąd wynika, że
. Stąd wynika, że
A) 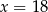 B)
B) 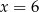 C)
C) 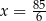 D)
D) 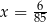
Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość 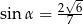 . Stąd wynika, że
. Stąd wynika, że
A) 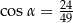 B)
B) 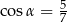 C)
C) 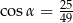 D)
D) 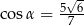
Na okręgu o środku w punkcie  leżą punkty
leżą punkty  i
i 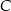 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 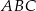 ma miarę
ma miarę 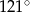 , a kąt
, a kąt 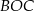 ma miarę
ma miarę 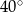 .
.
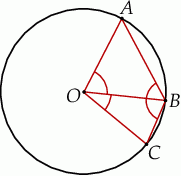
Kąt 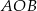 ma miarę
ma miarę
A) 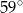 B)
B) 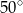 C)
C) 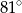 D)
D) 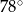
W trójkącie 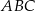 punkt
punkt 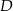 leży na boku
leży na boku 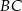 , a punkt
, a punkt 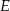 leży na boku
leży na boku 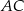 . Odcinek
. Odcinek 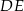 jest równoległy do boku
jest równoległy do boku 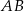 , a ponadto
, a ponadto 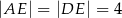 ,
, 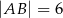 (zobacz rysunek).
(zobacz rysunek).
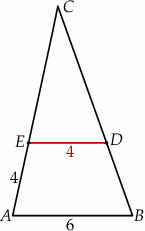
Odcinek 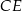 ma długość
ma długość
A) 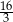 B)
B)  C) 8 D) 6
C) 8 D) 6
Dany jest trójkąt równoboczny, którego pole jest równe 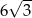 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 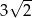 B)
B) 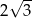 C)
C) 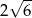 D)
D) 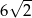
Punkty 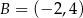 i
i 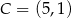 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 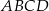 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 29 B) 40 C) 58 D) 74
Na rysunku przedstawiono ostrosłup prawidłowy czworokątny  o podstawie
o podstawie 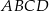 .
.
Kąt nachylenia krawędzi bocznej  ostrosłupa do płaszczyzny podstawy
ostrosłupa do płaszczyzny podstawy  to
to
A) 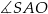 B)
B) 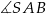 C)
C) 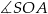 D)
D) 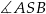
Graniastosłup ma 14 wierzchołków. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A) 14 B) 21 C) 28 D) 26
Prosta 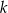 przechodzi przez punkt
przechodzi przez punkt 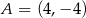 i jest prostopadła do osi
i jest prostopadła do osi 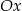 . Prosta
. Prosta 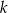 ma równanie
ma równanie
A) 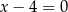 B)
B) 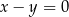 C)
C) 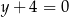 D)
D) 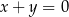
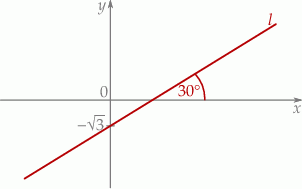
Prosta 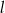 jest nachylona do osi
jest nachylona do osi 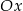 pod kątem
pod kątem 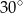 i przecina oś
i przecina oś 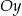 w punkcie
w punkcie 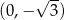 (zobacz rysunek).
(zobacz rysunek).
Prosta  ma równanie
ma równanie
A) 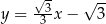 B)
B) 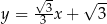 C)
C) 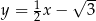 D)
D) 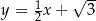
Dany jest stożek o wysokości 6 i tworzącej 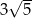 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 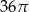 B)
B) 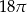 C)
C) 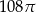 D)
D) 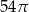
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 9 C) 10 D) 16
Ile jest wszystkich czterocyfrowych liczb naturalnych mniejszych niż 2017?
A) 2016 B) 2017 C) 1016 D) 1017
Z pudełka, w którym jest tylko 6 kul białych i  kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe 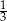 . Liczba kul czarnych jest równa
. Liczba kul czarnych jest równa
A) 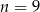 B)
B) 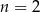 C)
C) 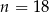 D)
D) 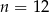
Zadania otwarte
Rozwiąż nierówność 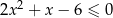 .
.
Rozwiąż równanie 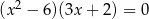 .
.
Udowodnij, że dla dowolnej dodatniej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
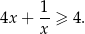
Dany jest trójkąt prostokątny 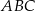 , w którym
, w którym 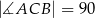 i
i 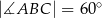 . Niech
. Niech 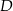 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 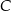 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 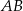 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 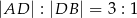 .
.
Ze zbioru liczb 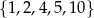 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 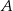 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
Dany jest ciąg arytmetyczny 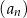 , określony dla
, określony dla 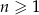 , w którym spełniona jest równość
, w którym spełniona jest równość 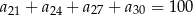 . Oblicz sumę
. Oblicz sumę 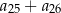 .
.
Funkcja kwadratowa 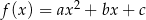 ma dwa miejsca zerowe
ma dwa miejsca zerowe 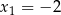 i
i 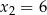 . Wykres funkcji
. Wykres funkcji 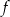 przechodzi przez punkt
przechodzi przez punkt 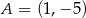 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 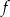 .
.
Punkt 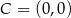 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 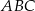 , którego wierzchołek
, którego wierzchołek 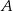 leży na osi
leży na osi 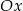 , a wierzchołek
, a wierzchołek 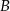 na osi
na osi 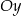 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 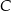 przecina przeciwprostokątną
przecina przeciwprostokątną 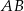 w punkcie
w punkcie 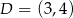 .
.
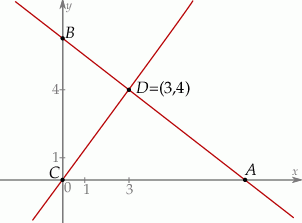
Oblicz współrzędne wierzchołków  i
i  tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej  .
.
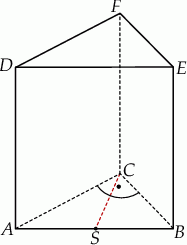
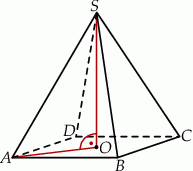
Podstawą graniastosłupa prostego 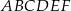 jest trójkąt prostokątny
jest trójkąt prostokątny 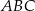 , w którym
, w którym 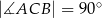 (zobacz rysunek). Stosunek długości przyprostokątnej
(zobacz rysunek). Stosunek długości przyprostokątnej 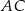 tego trójkąta do długości przyprostokątnej
tego trójkąta do długości przyprostokątnej 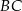 jest równy 4:3. Punkt
jest równy 4:3. Punkt 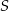 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 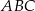 , a długość odcinka
, a długość odcinka 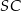 jest równa 5. Pole ściany bocznej
jest równa 5. Pole ściany bocznej 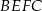 graniastosłupa jest równe 48. Oblicz objętość tego graniastosłupa.
graniastosłupa jest równe 48. Oblicz objętość tego graniastosłupa.