/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom rozszerzony 14 maja 2019 Czas pracy: 180 minut
Zadania zamknięte
Liczba 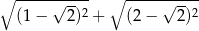 jest równa
jest równa
A) 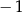 B)
B) 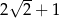 C) 1 D)
C) 1 D) 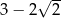
Wartość wyrażenia 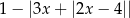 , dla
, dla 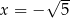 jest równa
jest równa
A) 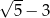 B)
B) 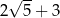 C)
C) 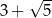 D)
D) 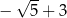
Liczba 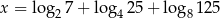 jest równa
jest równa
A) 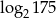 B)
B) 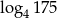 C)
C) 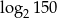 D)
D) 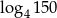
Liczba 0,3 jest jednym z przybliżeń liczby 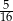 . Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
. Błąd względny tego przybliżenia, wyrażony w procentach, jest równy
A) 4% B) 0,04% C) 2,5% D) 0,025%
Dane są trzy okręgi o środkach 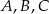 i promieniach równych odpowiednio
i promieniach równych odpowiednio 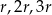 . Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli
. Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli 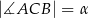 zaś
zaś 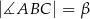 , to
, to
A) 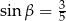 B)
B) 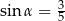 C)
C) 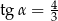 D)
D) 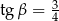
Zadania otwarte
Oblicz 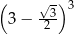 .
.
Rozwiąż równanie 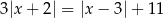 .
.
Uzasadnij, że jeżeli 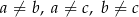 i
i 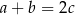 , to
, to 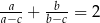 .
.
Wiedząc, że  , oblicz
, oblicz 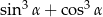 .
.
Wyznacz wszystkie liczby całkowite  , gdzie
, gdzie 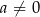 , dla których liczba
, dla których liczba 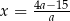 jest liczbą naturalną.
jest liczbą naturalną.
W trójkącie ostrokątnym 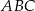 wysokości
wysokości 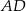 i
i 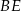 przecinają się w punkcie
przecinają się w punkcie 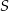 . Wiadomo, że
. Wiadomo, że 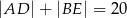 ,
, 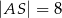 ,
, 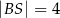 . Wyznacz długości odcinków
. Wyznacz długości odcinków 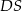 i
i 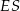 .
.
Dla jakich cyfr  i
i 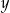
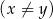 liczba
liczba 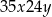 jest podzielna przez 45? (
jest podzielna przez 45? (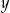 – jest to cyfra jedności, a
– jest to cyfra jedności, a  – cyfra tysięcy).
– cyfra tysięcy).
Dany jest prostokąt 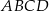 , w którym
, w którym 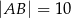 ,
, 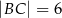 . Odcinek
. Odcinek 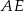 jest wysokością trójkąta
jest wysokością trójkąta 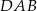 opuszczoną na jego bok
opuszczoną na jego bok 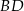 . Oblicz pole trójkąta
. Oblicz pole trójkąta 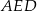 .
.
Uczniowie klasy 3a napisali prace klasową z matematyki. Oceny bardzo dobre otrzymało 30% uczniów, oceny dobre 40% uczniów, oceny dostateczne 8 uczniów, a pozostali uczniowie otrzymali oceny dopuszczające. Średnia ocen z tej klasówki wynosiła 3,9. Ilu uczniów otrzymało poszczególne oceny?
Dany jest trójkąt równoboczny 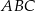 o boku długości 16. Na boku
o boku długości 16. Na boku 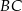 obrano punkt
obrano punkt 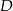 dzielący ten bok w stosunku 3:5, licząc od punktu
dzielący ten bok w stosunku 3:5, licząc od punktu 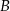 . Oblicz sinus kąta
. Oblicz sinus kąta 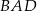 .
.
Wspólne styczne dwóch okręgów stycznych zewnętrznie przecinają się pod kątem 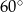 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.

