/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 25 kwietnia 2020 Czas pracy: 170 minut
Zadania zamknięte
Liczba 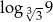 jest równa
jest równa
A) 4 B) 6 C) 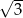 D)
D) 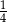
Jeżeli 37% liczby  jest równe 148 i 25% liczby
jest równe 148 i 25% liczby 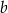 jest równe 148, to
jest równe 148, to
A) 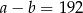 B)
B) 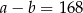 C)
C) 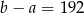 D)
D) 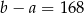
Jedną z liczb spełniających nierówność 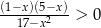 jest
jest
A) 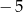 B)
B) 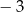 C)
C) 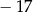 D)
D) 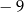
Liczba 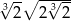 jest równa
jest równa
A) 2 B) 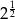 C)
C) 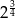 D)
D) 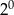
Para liczb 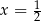 i
i 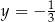 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 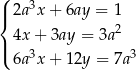 dla
dla
A) 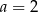 B)
B) 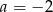 C)
C) 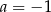 D)
D) 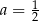
Równanie 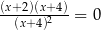 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 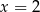 B) jedno rozwiązanie:
B) jedno rozwiązanie: 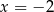
C) dwa rozwiązania: 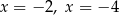 D) dwa rozwiązania:
D) dwa rozwiązania: 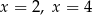
Funkcja 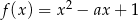 przyjmuje wartości mniejsze niż
przyjmuje wartości mniejsze niż 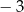 dla
dla
A) 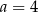 B)
B) 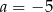 C)
C) 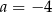 D)
D) 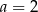
Rysunek przedstawia wykres funkcji 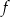 zbudowany z 6 odcinków.
zbudowany z 6 odcinków.
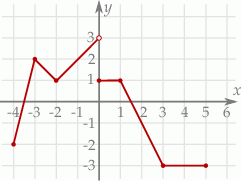
Równanie 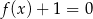 ma
ma
A) dokładnie jedno rozwiązanie. B) dokładnie dwa rozwiązania.
C) dokładnie trzy rozwiązania. D) nieskończenie wiele rozwiązań.
Najmniejszą wartość w przedziale 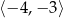 funkcja kwadratowa
funkcja kwadratowa 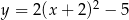 przyjmuje dla argumentu
przyjmuje dla argumentu
A) 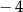 B)
B) 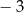 C)
C) 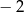 D)
D) 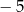
Punkt 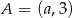 leży poniżej prostej określonej równaniem
leży poniżej prostej określonej równaniem 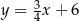 . Stąd wynika, że
. Stąd wynika, że
A) 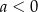 B)
B) 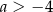 C)
C) 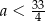 D)
D) 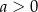
W ciągu arytmetycznym 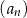 , określonym dla
, określonym dla 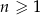 , dane są dwa wyrazy:
, dane są dwa wyrazy: 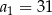 oraz
oraz 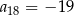 . Suma osiemnastu początkowych wyrazów tego ciągu jest równa
. Suma osiemnastu początkowych wyrazów tego ciągu jest równa
A) 102 B) 108 C) 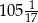 D)
D) 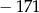
Kąt  jest ostry oraz wiadomo, że
jest ostry oraz wiadomo, że 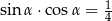 . Wartość wyrażenia
. Wartość wyrażenia 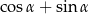 jest równa
jest równa
A) 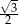 B)
B) 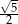 C)
C)  D)
D) 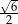
Odcinek 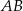 jest średnicą okręgu o środku
jest średnicą okręgu o środku 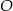 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 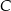 , taki, że
, taki, że 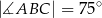 (zobacz rysunek).
(zobacz rysunek).
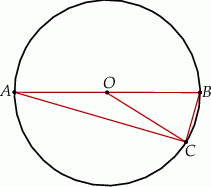
Pole trójkąta 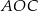 jest równe
jest równe
A) 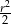 B)
B) 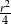 C)
C) 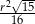 D)
D) 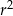
Wyrażenie 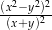 , gdzie
, gdzie 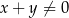 jest równe wyrażeniu
jest równe wyrażeniu
A) 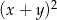 B)
B) 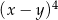 C)
C) 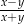 D)
D) 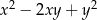
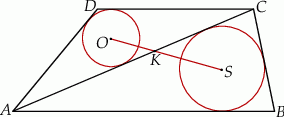
Trapez 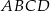 podzielono przekątną
podzielono przekątną 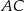 na dwa trójkąty. Punkty
na dwa trójkąty. Punkty 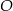 i
i 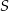 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty 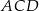 i
i 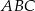 , a odcinek
, a odcinek 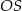 przecina przekątną
przecina przekątną 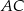 w punkcie
w punkcie 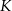 (zobacz rysunek). Stosunek długości okręgów o środkach
(zobacz rysunek). Stosunek długości okręgów o środkach 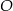 i
i 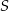 jest równy
jest równy 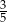 , a odcinek
, a odcinek 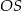 ma długość 24.
ma długość 24.
Wtedy
A) 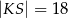 B)
B) 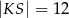 C)
C) 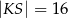 D)
D) 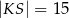
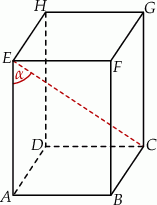
Podstawą graniastosłupa prostego czworokątnego 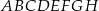 jest kwadrat
jest kwadrat 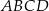 o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa
o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa 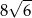 . Miara kąta
. Miara kąta 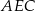 jest równa
jest równa
A) 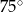 B)
B) 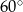 C)
C) 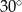 D)
D) 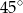
Ciągiem geometrycznym o ilorazie 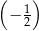 jest ciąg określony wzorem
jest ciąg określony wzorem
A) 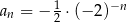 B)
B) 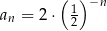 C)
C) 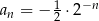 D)
D) 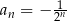
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 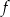 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 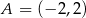 i
i 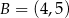 .
.
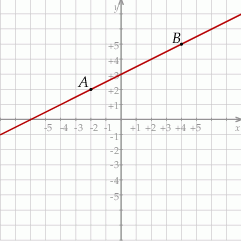
Obrazem prostej 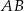 w symetrii względem początku układu współrzędnych jest wykres funkcji
w symetrii względem początku układu współrzędnych jest wykres funkcji 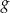 określonej wzorem
określonej wzorem
A) 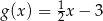 B)
B) 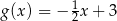 C)
C) 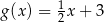 D)
D) 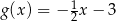
Punkt 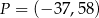 , przekształcono najpierw w symetrii względem osi
, przekształcono najpierw w symetrii względem osi 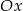 , a potem w symetrii względem osi
, a potem w symetrii względem osi 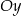 . W wyniku tych przekształceń otrzymano punkt
. W wyniku tych przekształceń otrzymano punkt 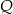 . Zatem
. Zatem
A) 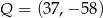 B)
B) 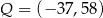 C)
C) 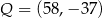 D)
D) 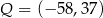
Suma długości wszystkich krawędzi czworościanu foremnego jest równa 12 cm. Pole powierzchni całkowitej tego czworościanu jest równe
A) 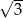 B)
B) 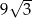 C)
C) 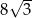 D)
D) 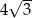
Liczba różnych wartości parametru  , dla których prosta
, dla których prosta 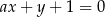 jest prostopadła do prostej
jest prostopadła do prostej 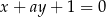 jest
jest
A) równa 0 B) równa 1 C) równa 2 D) większa od 2
Punkt 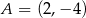 jest wierzchołkiem sześciokąta foremnego
jest wierzchołkiem sześciokąta foremnego 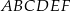 wpisanego w okrąg o środku
wpisanego w okrąg o środku 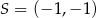 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 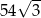 B)
B) 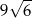 C)
C) 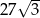 D)
D) 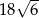
Dany jest zestaw danych: 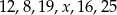 , gdzie
, gdzie  jest pewną liczbą całkowitą. Mediana tego zestawu danych nie może być równa
jest pewną liczbą całkowitą. Mediana tego zestawu danych nie może być równa
A) 14 B) 17,5 C) 13,5 D) 16,5
Liczba 99991 jest liczbą pierwszą. Liczba dzielników naturalnych liczby 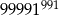 jest równa
jest równa
A) 1982 B) 990 C) 991 D) 992
Ze zbioru kolejnych liczb naturalnych 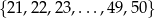 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
A) 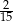 B)
B)  C)
C) 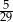 D)
D) 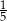
Zadania otwarte
Funkcje 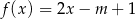 i
i 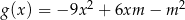 mają wspólne miejsce zerowe. Oblicz
mają wspólne miejsce zerowe. Oblicz 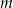 .
.
Rozwiąż nierówność 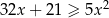 .
.
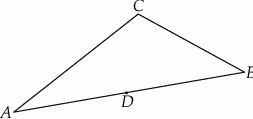
Na boku 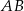 trójkąta
trójkąta 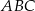 wybrano punkt
wybrano punkt 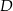 w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 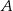 i
i 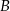 od prostej
od prostej 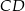 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 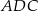 i
i 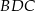 mają równe pola.
mają równe pola.
Wykaż, że dla każdej liczby 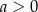 i dla każdej liczby
i dla każdej liczby 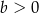 prawdziwa jest nierówność
prawdziwa jest nierówność
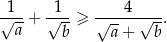
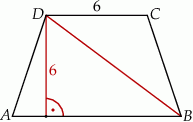
W trapezie równoramiennym 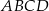 krótsza podstawa
krótsza podstawa 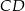 ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy
ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy 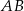 jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
Punkty 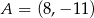 i
i 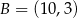 są końcami cięciwy okręgu o środku
są końcami cięciwy okręgu o środku 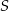 . Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt
. Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt 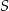 .
.
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 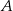 polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
W ciągu geometrycznym 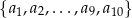 iloczyn wyrazów o numerach parzystych jest równy
iloczyn wyrazów o numerach parzystych jest równy 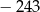 , a iloczyn wyrazów o numerach nieparzystych jest równy 7776. Wyznacz ostatni wyraz tego ciągu geometrycznego.
, a iloczyn wyrazów o numerach nieparzystych jest równy 7776. Wyznacz ostatni wyraz tego ciągu geometrycznego.
Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego 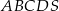 jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt
jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt  taki, że
taki, że 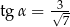 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.