Zadanie nr 4073269
Doświadczenie losowe polega na tym, że losujemy bez zwracania trzy liczby ze zbioru 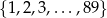 . Oblicz prawdopodobieństwo, że wśród wylosowanych liczb jest liczba parzysta, jeżeli wiadomo, że pierwsza z wylosowanych liczb jest nieparzysta.
. Oblicz prawdopodobieństwo, że wśród wylosowanych liczb jest liczba parzysta, jeżeli wiadomo, że pierwsza z wylosowanych liczb jest nieparzysta.
Rozwiązanie
Sposób I
Jeżeli wiemy, że pierwsza z wylosowanych liczb jest nieparzysta, to pozostałe dwie losujemy ze zbioru, w którym są 44 liczby parzyste i 44 liczby nieparzyste. Prawdopodobieństwo wybrania kolejnych dwóch liczb nieparzystych jest więc równe
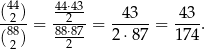
W takim razie interesujące nas prawdopodobieństwo otrzymania przynajmniej jednej liczby parzystej jest równe
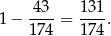
Sposób II
Za zdarzenia elementarny przyjmijmy uporządkowane trójki 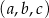 wylosowanych liczb. W szczególności
wylosowanych liczb. W szczególności
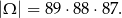
Niech 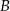 będzie zdarzeniem polegającym na wylosowaniu pierwszej liczby nieparzystej, a
będzie zdarzeniem polegającym na wylosowaniu pierwszej liczby nieparzystej, a 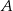 zdarzeniem polegającym na otrzymaniu przynajmniej jednej liczby parzystej. Interesuje nas prawdopodobieństwo warunkowe
zdarzeniem polegającym na otrzymaniu przynajmniej jednej liczby parzystej. Interesuje nas prawdopodobieństwo warunkowe
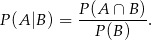
W zdarzeniach sprzyjających zdarzeniu 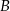 wybieramy najpierw liczbę nieparzystą – możemy to zrobić na 45 sposobów, a potem dobieramy do niej dwie dowolne liczby z pozostałych 88 liczb. Mamy więc
wybieramy najpierw liczbę nieparzystą – możemy to zrobić na 45 sposobów, a potem dobieramy do niej dwie dowolne liczby z pozostałych 88 liczb. Mamy więc
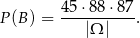
Zdarzenia sprzyjające zdarzeniu 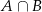 są dwóch rodzajów – albo wylosowaliśmy dwie liczby parzyste, albo tylko jedną. Zdarzeń pierwszego typu jest
są dwóch rodzajów – albo wylosowaliśmy dwie liczby parzyste, albo tylko jedną. Zdarzeń pierwszego typu jest
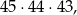
(wybieramy liczbę nieparzystą na pierwszym miejscu, a potem dwie liczby parzyste), a zdarzeń drugiego typu jest
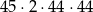
(wybieramy liczbę nieparzystą na pierwszym miejscu, wybieramy miejsce liczby parzystej, wybieramy tę liczbę parzystą i w końcu wybieramy drugą liczbę nieparzystą). Mamy więc
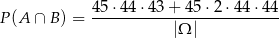
Interesujące nas prawdopodobieństwo jest więc równe
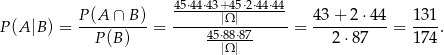
Odpowiedź: