/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2020/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 4 kwietnia 2020 Czas pracy: 100 minut
Bartek postanowił niektórym liczbom naturalnym przyporządkować kolory – wszystkim liczbom podzielnym przez 18 przyporządkował kolor czerwony, a wszystkim liczbom podzielnym przez 24 kolor zielony.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Najmniejszą liczbą, która jest jednocześnie czerwona i zielona jest 144. | P | F |
Największą czerwoną liczbą trzycyfrową jest 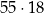 . . | P | F |
Liczba 1300 jest zaokrągleniem do rzędu setek różnych liczb naturalnych.
Ile jest wszystkich liczb naturalnych różnych od 1300, które mają takie zaokrąglenie? Wybierz właściwą odpowiedź spośród podanych.
A) 100 B) 99 C) 49 D) 50
Wiadomo, że 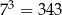 i
i 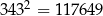 .
.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba 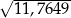 jest równa A/B .
jest równa A/B .
A) 3,43 B) 0,343
Liczba 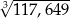 jest równa C/D .
jest równa C/D .
C) 0,49 D) 4,9
Dane są cztery wyrażenia:
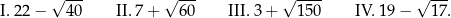
Wartości których wyrażeń są większe od 15? Wybierz właściwą odpowiedź spośród podanych.
A) I i III B) II i III C) III i IV D) I, IV
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 3069792 jest liczbą podzielną przez 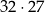 . . | P | F |
Liczba 3069792 nie jest podzielna przez 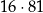 . . | P | F |
Agata przygotowuje 5-procentowy roztwór soli do kiszenia ogórków.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Agata do 4,75 kg wody musi dodać A/B soli aby otrzymać żądany roztwór.
A) 237,5 g B) 250 g
W 1 kg otrzymanego roztworu jest C/D soli.
C) 52,6 g D) 50 g
Średnia cena sześciu kartonów mleka po 3,2 zł za karton i dwóch identycznych pojemników śmietany wynosi 2,85 zł.
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Cena jednego pojemnika śmietany jest równa
A) 1,8 zł B) 3,6 zł C) 2 zł D) 2,4 zł
Dane jest wyrażenie 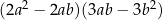 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dane wyrażenie jest równe wyrażeniu 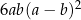 . . | P | F |
Dane wyrażenie jest równe wyrażeniu 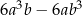 . . | P | F |
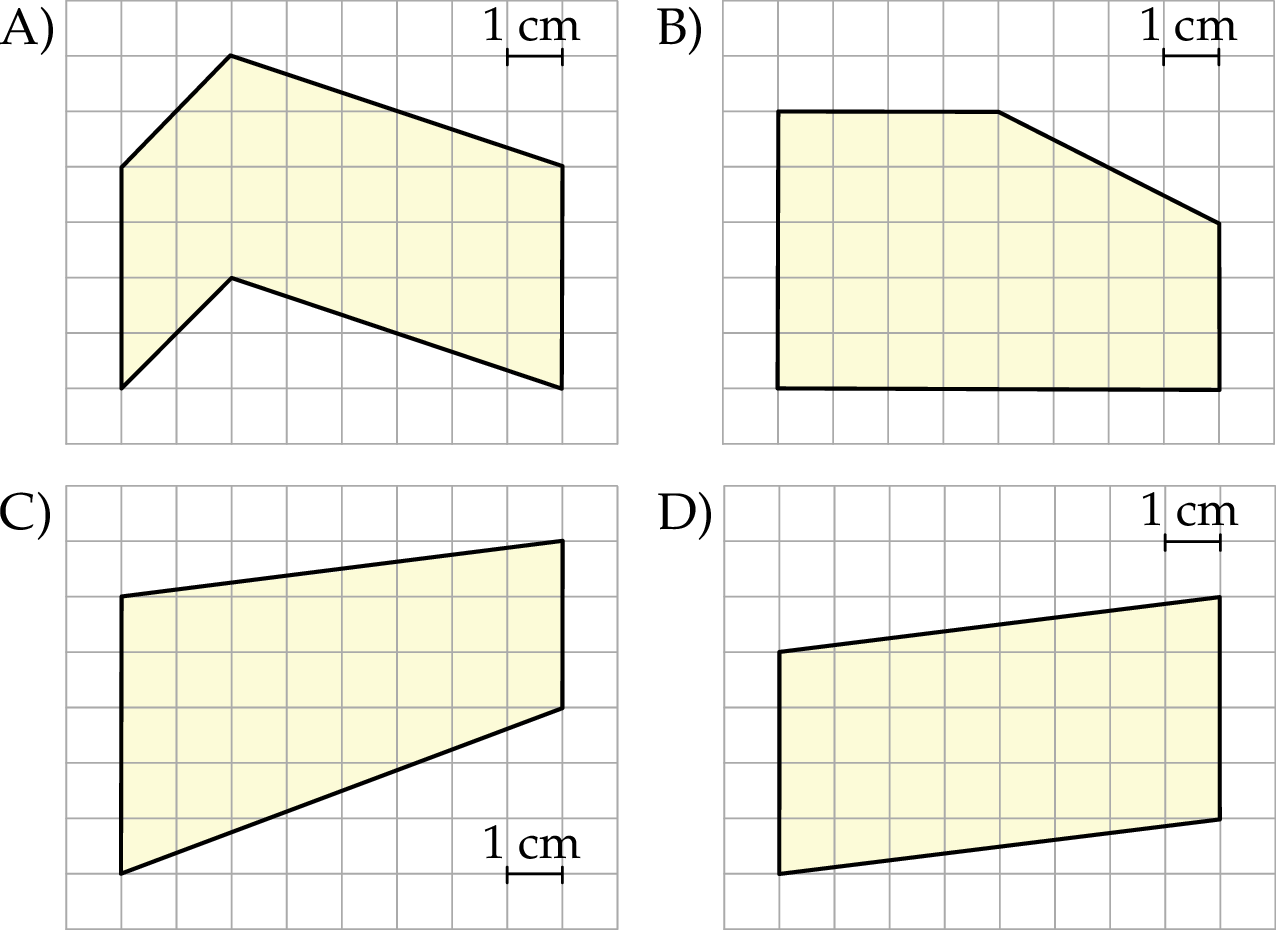
Na rysunkach zaznaczono cztery wielokąty o wierzchołkach w punktach przecięcia się linii siatki. Wskaż wielokąt, którego pole jest inne niż pola trzech pozostałych wielokątów.
Kwadrat o boku  przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II – jeden z prostokątów nałożono na drugi prostokąt.
przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II – jeden z prostokątów nałożono na drugi prostokąt.
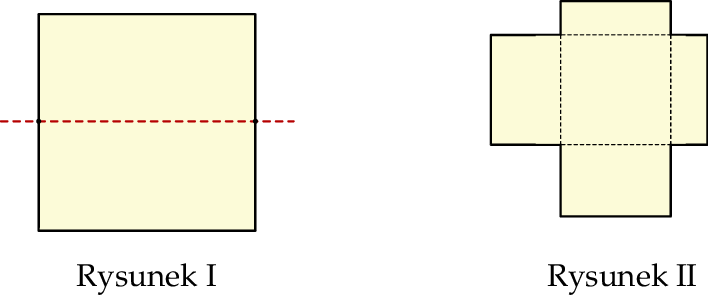
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód ułożonej figury jest dwa razy większy od obwodu kwadratu. | P | F |
Pole ułożonej figury jest równe 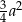 . . | P | F |
W koszu znajdowały się jednakowe sześcienne klocki, których ściany są kwadratami o polu powierzchni 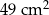 . Z wszystkich tych klocków zbudowano prostopadłościan o objętości
. Z wszystkich tych klocków zbudowano prostopadłościan o objętości 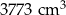 .
.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W koszu znajdowało się A/B klocków.
A) 11 B) 77
Pole powierzchni całkowitej zbudowanego prostopadłościanu jest równe C/D .
C) 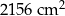 D)
D) 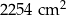
Na rysunku przedstawiono równoległobok  i trójkąt równoramienny
i trójkąt równoramienny  , w którym
, w którym 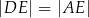 . Miara kąta
. Miara kąta 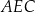 jest równa
jest równa 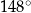 .
.

Jaką miarę ma kąt 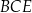 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) 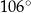 B)
B) 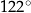 C)
C) 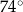 D)
D) 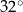
Informacja do zadań 13 i 14
Wysokość 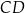 trójkąta
trójkąta 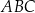 ma długość 12, bok
ma długość 12, bok 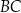 ma długość 37, a odcinek
ma długość 37, a odcinek 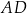 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
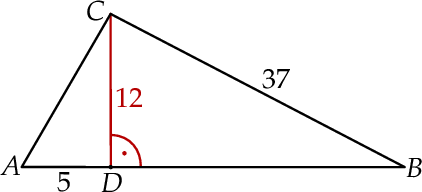
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Pole trójkąta 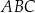 jest równe A/B .
jest równe A/B .
A) 240 B) 210
Obwód trójkąta 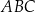 jest równy C/D .
jest równy C/D .
C) 90 D) 120
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 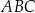 jest prostokątny. jest prostokątny. | P | F |
Miara kąta 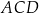 jest równa jest równa 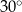 . . | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Ostrosłup o 2020 ścianach ma A/B krawędzi.
A) 4038 B) 4040
Graniastosłup o 2020 wierzchołkach ma C/D ścian.
C) 1010 D) 1012
Na diagramie przedstawiono informacje, jaki procent meczów w ciągu całego sezonu drużyna siatkarska zakończyła wygraną, jaki – przegraną, a jaki – remisem.
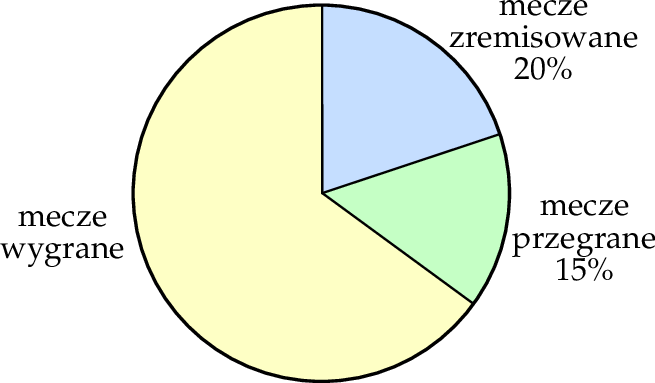
W ciągu całego sezonu drużyna przegrała 3 mecze. Ile meczów w sezonie ta drużyna wygrała?
Prostokątną działkę o powierzchni 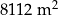 podzielono na pięć prostokątnych działek o jednakowych wymiarach i dwie działki w kształcie kwadratu (zobacz rysunek).
podzielono na pięć prostokątnych działek o jednakowych wymiarach i dwie działki w kształcie kwadratu (zobacz rysunek).
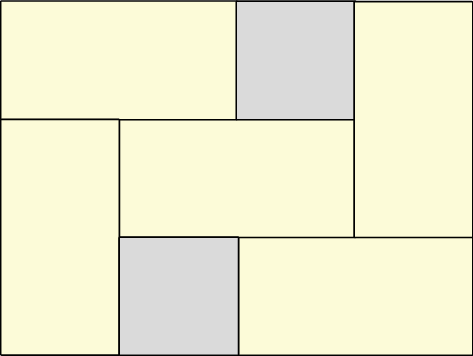
Jakie wymiary miała działka przed podziałem?
Właściciele trzech firm budowlanych zamówili w hurtowni cement: pan Henryk – 3200 kg, pan Józef – 2200 kg, pan Kamil – 4600 kg. Problem z zaopatrzeniem sprawił, że hurtownia miała w sprzedaży tylko 8 ton cementu. W jaki sposób hurtownia powinna skorygować opisane zamówienia tak, aby proporcje liczb kilogramów cementu otrzymanego przez poszczególne firmy budowalne były takie same jak w pierwotnym zamówieniu.
W pierwszej urnie znajduje się 5 kul białych i 17 kul czarnych. W drugiej urnie znajduje się 16 kul białych i 34 kule czarne. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
Z wierzchołka kąta prostego trójkąta prostokątnego 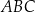 poprowadzono wysokość
poprowadzono wysokość 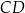 , która podzieliła przeciwprostokątną
, która podzieliła przeciwprostokątną 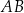 na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
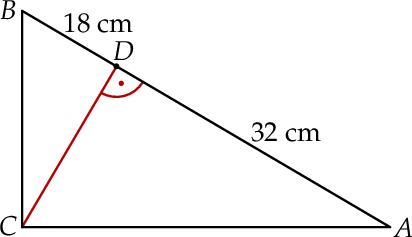
Oblicz pole trójkąta  .
.
Oblicz objętość graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 16 cm i 30 cm, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy.

