/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2020/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 18 kwietnia 2020 Czas pracy: 100 minut
Do udziału w podchodach zgłosiło się 54 chłopców i 24 dziewczynki. Uczestników postanowiono podzielić na zespoły w ten sposób, aby we wszystkich zespołach była ta sama liczba dziewcząt i ta sama liczba chłopców.
Ile maksymalnie zespołów utworzono? Wybierz odpowiedź spośród podanych.
A) 9 B) 2 C) 3 D) 6
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Na osi liczbowej narysowano odcinek, którego końcami są największa i najmniejsza spośród liczb 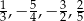 . Długość tego odcinka jest równa
. Długość tego odcinka jest równa
A) 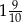 B)
B) 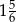 C)
C) 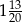 D)
D) 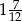
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Co trzeci uczeń biorący udział w zawodach był uczniem klasy trzeciej, co czwarty był uczniem klasy piątej, a pozostałych 15 uczniów było uczniami klasy czwartej. W zawodach brało udział
A) 28 uczniów. B) 32 uczniów. C) 36 uczniów. D) 48 uczniów.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
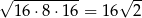 | P | F |
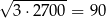 | P | F |
Informacja do zadań 5 i 6
W trakcie dziesięciu godzin otwarcia sklepu, właściciel prowadził obserwację liczby klientów, którzy odwiedzili ten sklep. Wynik tej obserwacji przedstawiono na wykresie.
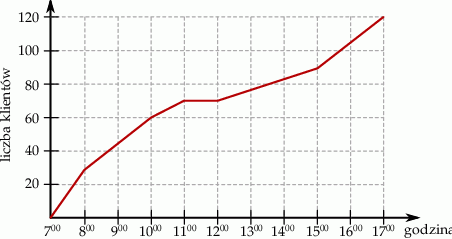
Na podstawie wykresu wybierz zdanie fałszywe.
A) Od 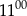 do
do 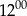 do sklepu nie przyszedł żaden klient.
do sklepu nie przyszedł żaden klient.
B) W godzinach od 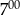 do
do 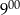 sklep odwiedziło mniej klientów niż od
sklep odwiedziło mniej klientów niż od 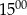 do
do 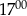 .
.
C) W ciągu pierwszej godziny sklep odwiedziło więcej klientów niż w ciągu drugiej godziny.
D) W ciągu trzech pierwszych godzin pracy sklep odwiedziło tylu samo klientów, co w ciągu pozostałych godzin pracy.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnio w ciągu jednej godziny obserwacji sklep odwiedzało 12 klientów. | P | F |
| Gdyby właściciel zakończył obserwację po 8 godzinach to średnia liczba klientów w ciągu godziny byłaby wyższa. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Cena książki po podwyżce o 20% wynosi 84 zł. Cena tej książki przed podwyżką była równa
A) 70 zł. B) 56 zł. C) 67,20 zł. D) 82,35 zł.
Informacja do zadań 8 i 9
Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 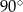 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
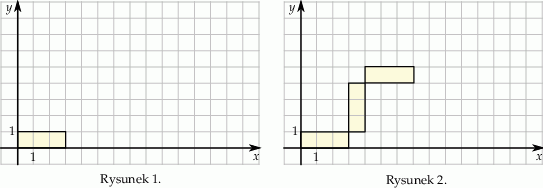
Oceń prawdziwość podanych zdań.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli punkt 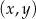 jest prawym górnym wierzchołkiem 20 prostokąta to
jest prawym górnym wierzchołkiem 20 prostokąta to
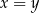 | P | F |
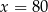 | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Współrzędne prawego górnego wierzchołka 39 prostokąta są równe 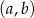 . Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe
. Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe
A) 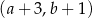 B)
B) 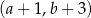 C)
C) 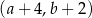 D)
D) 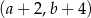
W trójkącie 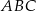 , w którym
, w którym 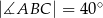 ,
, 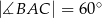 poprowadzono dwusieczne
poprowadzono dwusieczne 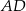 i
i 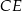 , które przecinają się w punkcie
, które przecinają się w punkcie 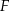 .
.
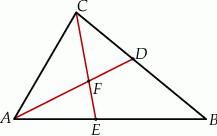
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
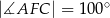 | P | F |
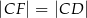 | P | F |
Z 9 sześcianów o krawędziach długości 2 zbudowano graniastosłup prawidłowy czworokątny. Które wymiary, z podanych w tabeli, może mieć ten graniastosłup? Wybierz odpowiedź spośród A–E.
| I | 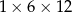 |
| II | 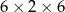 |
| III | 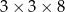 |
| IV | 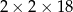 |
| V | 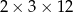 |
A) II, III i IV B) III i IV C) II i IV D) Wszystkie podane.
Dwie proste równoległe 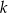 i
i 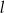 przecięto prostymi
przecięto prostymi 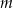 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
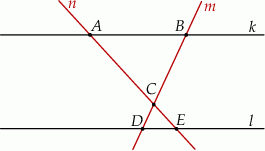
Czy trójkąty 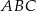 i
i 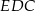 są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
| D) | te trójkąty mają boki równoległe. |
Od kartonika w kształcie trójkąta równobocznego odcięto naroża, tak jak pokazano na rysunku i otrzymano sześciokąt foremny o bokach długości 3.
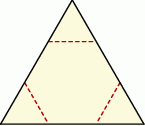
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był trójkątem o obwodzie 27. | P | F |
| Suma pól odciętych naroży jest dwa razy mniejsza od pola sześciokąta. | P | F |
Dany jest trapez prostokątny 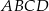 , w którym trójkąt
, w którym trójkąt 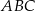 jest trójkątem równobocznym o boku długości 6 cm.
jest trójkątem równobocznym o boku długości 6 cm.
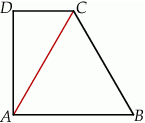
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
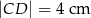 | P | F |
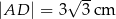 | P | F |
Który z poniższych rysunków nie może być siatką sześcianu? Wybierz odpowiedź spośród podanych.
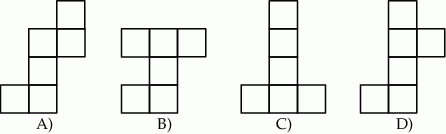
Asia napisała na tablicy liczbę trzycyfrową, która jest podzielna przez 45, i w której zapisie występują tylko dwie różne cyfry. Jaką liczbę mogła napisać Asia? Podaj wszystkie możliwości. Odpowiedź uzasadnij.
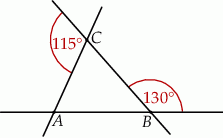
Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt 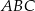 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 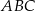 jest równoramienny.
jest równoramienny.
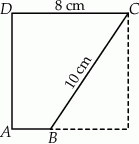
Z kwadratu o boku długości 8 cm wycięto trójkąt prostokątny o przeciwprostokątnej długości 10 cm w sposób pokazany na rysunku. Oblicz pole otrzymanego czworokąta 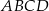 . Zapisz obliczenia.
. Zapisz obliczenia.
Troje przyjaciół: Adam, Wojtek i Karol postanowiło kupić losy na loterii, w której jeden los kosztował 4 zł. Adam kupił 12 losów, Wojtek kupił 9 losów, a Karol kupił 3 losy. Po sprawdzeniu wszystkich losów okazało się, że chłopcy wygrali w sumie 168 zł. Wygraną kwotę postanowili podzielić następująco: każdy z chłopców z wygranej kwoty zabrał tyle pieniędzy, ile wydał na losy, a pozostałą kwotę chłopcy podzieli między siebie, proporcjonalnie do liczby kupionych losów. Ile pieniędzy z wygranych 168 zł otrzymał każdy z chłopców? Zapisz obliczenia.
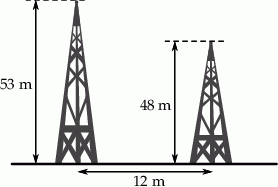
Dwa stalowe maszty o wysokościach 48 m i 53 m stoją w odległości 12 metrów od siebie. Czubki tych masztów postanowiono połączyć stalową liną, której 1 metr waży 500 g. Jaka będzie waga liny łączącej czubki masztów? Wynik podaj w kilogramach. Zapisz obliczenia.
Na rysunku przedstawiono bryłę, której każda ściana jest albo kwadratem, albo trójkątem równobocznym. Kwadratami są też czworokąty 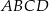 i
i 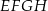 . Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
. Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.