/Szkoła średnia/Zadania maturalne/Matura 2020/XII Polygon Matematyczny

Stereometria – bryły obrotowe poziom rozszerzony

Zadanie 1

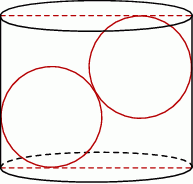
W pojemniku o kształcie walca o promieniu podstawy 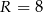R = 8 umieszczono dwie kule o promieniu 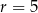r = 5 , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.

Zadanie 2

Trójkąt o bokach 3, 5, 7 jest podstawą graniastosłupa prostego, w który wpisano kulę. Oblicz objętość tego graniastosłupa.

Zadanie 3

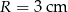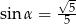Metalową kulę o promieniu R = 3 cm przetopiono na stożek. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem , takim, że √ - sin α = -55 . Wyznacz promień podstawy tego stożka.

Zadanie 4

W sferę o promieniu 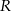wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość 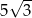√ -- 5 3 , oblicz .

Zadanie 5

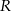W kulę o promieniu 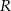wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem . Oblicz objętość stożka.

Zadanie 6

Podstawa stożka o kącie rozwarcia 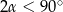2α < 90∘ jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu .

Zadanie 7

Do sześciennego pudła o boku długości 60 cm, włożono walec, który jest styczny do przylegających ścian. Jak dużą kulkę można jeszcze zmieścić w wolnym rogu pudła?

Zadanie 8

Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości stożka do objętości walca wynosi 8 : 3. Oblicz tangens kąta zawartego między wysokością a tworzącą stożka.

Wersja PDF