Zadanie nr 8497261
Punkty 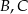 i
i 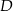 leżą na okręgu o środku
leżą na okręgu o środku 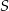 i promieniu
i promieniu  . Punkt
. Punkt 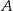 jest punktem wspólnym prostych
jest punktem wspólnym prostych 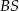 i
i 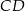 , a odcinki
, a odcinki 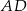 i
i 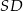 są równej długości. Miara kąta
są równej długości. Miara kąta 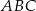 jest równa
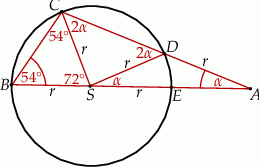
jest równa 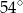 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
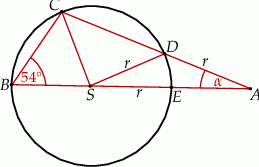
A) 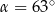 B)
B) 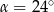 C)
C) 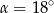 D)
D) 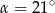
Rozwiązanie
Zauważmy najpierw, że każdy z odcinków 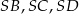 ma długość równą promieniowi okręgu.
ma długość równą promieniowi okręgu.
W szczególności trójkąt 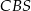 jest równoramienny i
jest równoramienny i
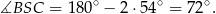
Z założenia trójkąt 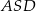 też jest równoramienny, więc
też jest równoramienny, więc
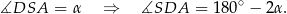
To z kolei oznacza, że
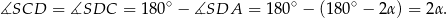
Stąd
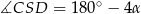
i
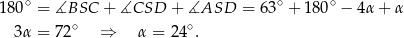
Odpowiedź: B

