Zadanie nr 5721752
Podstawą ostrosłupa 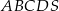 jest prostokąt
jest prostokąt 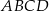 , którego boki mają długości
, którego boki mają długości 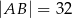 i
i 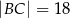 . Ściany boczne
. Ściany boczne 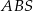 i
i 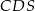 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem  . Ściany boczne
. Ściany boczne 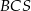 i
i 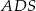 są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem
są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem 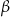 . Miary kątów
. Miary kątów  i
i 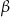 spełniają warunek:
spełniają warunek: 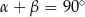 . Oblicz
. Oblicz 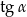 oraz pole powierzchni całkowitej tego ostrosłupa.
oraz pole powierzchni całkowitej tego ostrosłupa.
Rozwiązanie
Zaczynamy od rysunku.
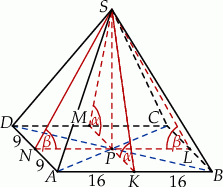
Niech 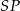 będzie wysokością ostrosłupa, a
będzie wysokością ostrosłupa, a 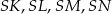 niech będą wysokościami ścian bocznych. Wtedy płaszczyzny
niech będą wysokościami ścian bocznych. Wtedy płaszczyzny 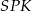 ,
, 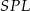 ,
, 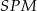 ,
, 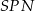 są prostopadłe do odpowiednich krawędzi podstawy i to pozwala łatwo zidentyfikować kąty nachylenia ścian bocznych płaszczyzny podstawy:
są prostopadłe do odpowiednich krawędzi podstawy i to pozwala łatwo zidentyfikować kąty nachylenia ścian bocznych płaszczyzny podstawy: 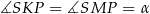 i
i 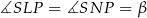 . W szczególności trójkąty prostokątne
. W szczególności trójkąty prostokątne 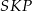 i
i 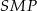 są przystające i
są przystające i 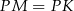 . Analogicznie, przystające są trójkąty
. Analogicznie, przystające są trójkąty 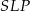 i
i 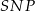 , czyli
, czyli 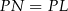 . To oznacza, że punkt
. To oznacza, że punkt 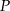 jest środkiem prostokąta
jest środkiem prostokąta 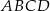 . To z kolei oznacza, że
. To z kolei oznacza, że 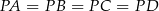 i trójkąty
i trójkąty 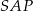 ,
, 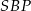 ,
, 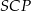 i
i 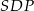 są przystające. Stąd
są przystające. Stąd 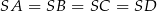 , czyli wszystkie trójkąty w ścianach bocznych są równoramienne.
, czyli wszystkie trójkąty w ścianach bocznych są równoramienne.
Zauważmy, że podana informacja o przystawaniu przeciwległych ścian bocznych jest zupełnie niepotrzebna – wynika to z równości kątów nachylenia przeciwległych ścian bocznych do płaszczyzny podstawy.
Spróbujemy teraz wykorzystać podaną informację o tym, że 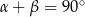 . W trójkątach prostokątnych
. W trójkątach prostokątnych 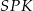 i
i 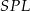 mamy
mamy
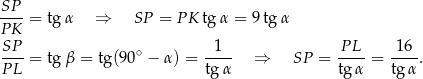
Stąd
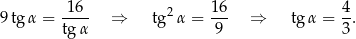
Stąd 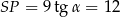 i
i
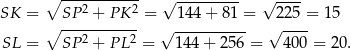
Teraz już łatwo obliczyć pole powierzchni całkowitej ostrosłupa.
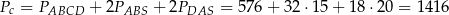
Odpowiedź: 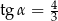 ,
,