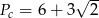/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Prostokąt w podstawie

Zadanie nr 9421365

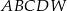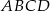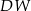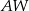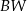Podstawą ostrosłupa ABCDW jest kwadrat ABCD . Krawędź boczna DW jest wysokością tego ostrosłupa. Krawędzie boczne AW i BW mają następujące długości: 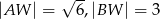√ -- |AW | = 6,|BW | = 3 . Oblicz pole powierzchni całkowitej tego ostrosłupa.

PIC

Wersja PDF

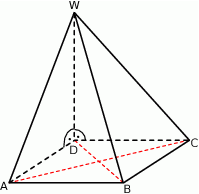
Rozwiązanie

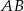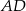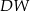Zauważmy, że krawędź AB jest prostopadła do AD i do DW (bo jest równoległa do 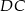DC ). To oznacza, że krawędź 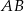AB jest prostopadła do płaszczyzny 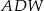ADW . Jest więc prostopadła do każdej prostej zawartej w tej płaszczyźnie, w szczególności trójkąt 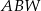ABW jest prostokątny. Mamy więc

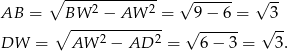
------------- ∘ 2 2 √ ------ √ -- AB = ∘BW---−--AW---= √9−--6-= √3-- DW = AW 2 − AD 2 = 6− 3 = 3.

Pole powierzchni całkowitej jest więc równe

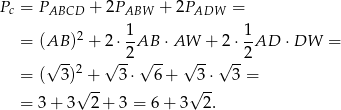
Pc = PABCD + 2PABW + 2PADW = = (AB )2 + 2⋅ 1AB ⋅AW + 2 ⋅ 1AD ⋅ DW = √ -- √ -2 √ -- √ --√ --2 = ( 3)2 + 3⋅ 6+ 3⋅ 3 = √ -- √ -- = 3+ 3 2 + 3 = 6 + 3 2 .

 
Odpowiedź: P = 6 + 3√ 2- c

Wersja PDF