Zadanie nr 9546185
Podstawą ostrosłupa 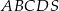 jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość
jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 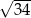 . Krawędź
. Krawędź 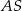 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 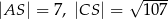 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Rozwiązanie
Na początku próbujemy naszkicować opisaną sytuację – jest z tym jednak pewien kłopot, bo nie wiemy, ani które krawędzie podstawy są podstawami trapezu, ani też, przy których wierzchołkach są kąty proste trapezu.
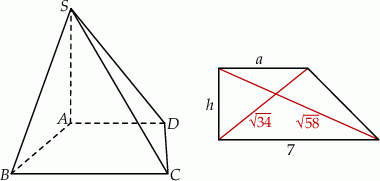
Aby to ustalić zauważmy, że z podanych danych możemy obliczyć długość przekątnej 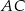 trapezu.
trapezu.
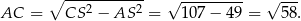
Wiemy, że jedna z przekątnych trapezu ma długość 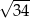 , więc
, więc 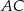 musi być drugą, dłuższą przekątną. Zauważmy ponadto, że
musi być drugą, dłuższą przekątną. Zauważmy ponadto, że 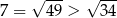 , więc podstawa długości 7 jest dłuższą podstawą trapezu. To pozwala nam dokładniej zająć się tym trapezem – łatwo możemy teraz obliczyć wysokość trapezu.
, więc podstawa długości 7 jest dłuższą podstawą trapezu. To pozwala nam dokładniej zająć się tym trapezem – łatwo możemy teraz obliczyć wysokość trapezu.
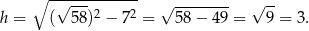
Następnie obliczamy długość krótszej podstawy
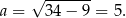
Obliczamy pole trapezu.
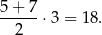
Objętość ostrosłupa jest więc równa
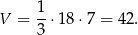
Odpowiedź: 42

