/Szkoła średnia/Zadania maturalne/Matura 2021
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 13 marca 2021 Czas pracy: 170 minut
Zadania zamknięte
Wyrażenie 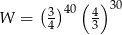 jest równe
jest równe
A) 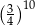 B)
B) 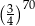 C) 1 D)
C) 1 D) 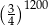
Liczbę 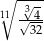 można zapisać w postaci
można zapisać w postaci
A) 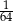 B)
B) 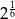 C)
C) 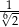 D)
D) 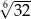
Rozwiązaniem równania 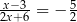 jest liczba
jest liczba
A) 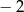 B) 2 C) 4 D)
B) 2 C) 4 D) 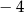
Cenę  pewnego towaru dwukrotnie obniżono o 50% i otrzymano cenę
pewnego towaru dwukrotnie obniżono o 50% i otrzymano cenę 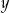 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 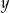 należy podnieść o
należy podnieść o
A) o 100% B) o 300% C) o 75% D) o 200%
Liczba ![[ ] log log (log√ -4) 4 16 2](https://img.zadania.info/zes/0070465/HzesT16x.gif) jest równa
jest równa
A) 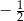 B)
B) 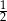 C)
C) 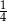 D) 2
D) 2
Jeżeli 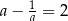 , to liczba
, to liczba 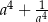 jest równa
jest równa
A) 36 B) 34 C) 6 D) 16
Na rysunkach przedstawione są wykresy funkcji 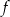 i
i 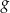 .
.
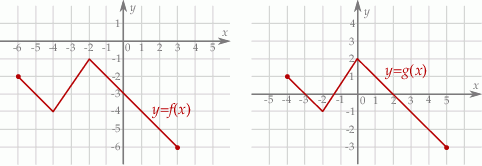
Wykres funkcji 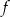 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 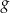 , zatem
, zatem
A) 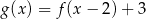 B)
B) 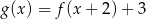
C) 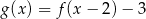 D)
D) 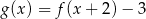
Funkcja 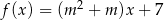 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 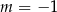 B)
B) 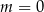 C)
C) 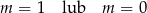 D)
D) 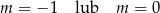
Przedział 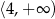 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 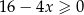 B)
B) 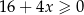 C)
C) 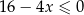 D)
D) 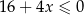
Równanie 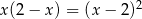 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie: 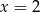
C) ma dokładnie jedno rozwiązanie: 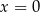
D) ma dwa różne rozwiązania: 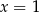 i
i 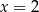
Rozwiązanie 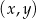 układu równań
układu równań 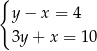 spełnia warunki
spełnia warunki
A) 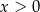 i
i 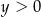 B)
B) 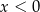 i
i 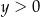 C)
C) 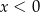 i
i 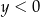 D)
D) 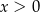 i
i 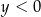
Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej 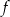 określonej wzorem
określonej wzorem 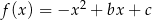 . Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne
. Wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne 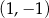 .
.
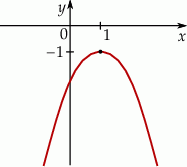
Stąd wynika, że:
A) 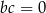 B)
B) 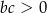 C)
C) 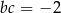 D)
D) 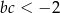
Prosta 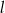 jest równoległa do prostej
jest równoległa do prostej 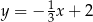 . Na prostej
. Na prostej 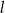 leży punkt
leży punkt 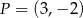 . Zatem równanie prostej
. Zatem równanie prostej 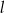 ma postać
ma postać
A) 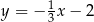 B)
B) 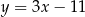 C)
C) 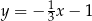 D)
D) 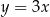
Ciąg 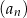 spełnia warunek
spełnia warunek 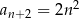 dla
dla 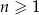 . Różnica
. Różnica 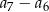 jest równa
jest równa
A) 26 B) 20 C) 36 D) 18
Jeżeli 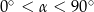 oraz
oraz 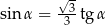 , to
, to
A) 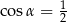 B)
B) 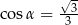 C)
C) 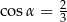 D)
D) 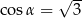
Mediana danych 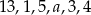 jest równa 4. Wówczas
jest równa 4. Wówczas
A) 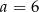 B)
B) 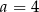 C)
C) 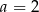 D)
D) 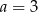
Dany jest ciąg geometryczny 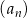 , określony dla
, określony dla 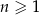 , o którym wiemy, że:
, o którym wiemy, że: 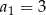 i
i 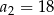 . Wtedy
. Wtedy 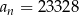 dla
dla
A) 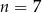 B)
B) 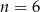 C)
C) 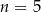 D)
D) 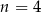
Prosta przechodząca przez punkty 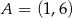 i
i 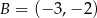 jest określona równaniem
jest określona równaniem
A) 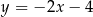 B)
B) 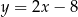 C)
C) 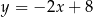 D)
D) 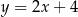
Wszystkie wyrazy rosnącego ciągu arytmetycznego 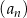 , gdzie
, gdzie 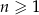 są dodatnimi liczbami całkowitymi. Jeżeli
są dodatnimi liczbami całkowitymi. Jeżeli 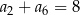 , to suma dziesięciu początkowych wyrazów ciągu
, to suma dziesięciu początkowych wyrazów ciągu 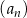 jest równa
jest równa
A) 45 B) 66 C) 55 D) 48
Metalowa płyta ma kształt trójkąta równoramiennego o wysokości 4 dm, którego ramię jest nachylone do podstawy pod kątem  . Powierzchnia płyty jest równa
. Powierzchnia płyty jest równa
A) 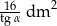 B)
B) 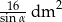 C)
C) 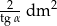 D)
D) 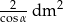
Na okręgu o środku w punkcie 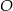 leżą punkty
leżą punkty 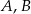 i
i 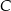 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 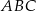 ma miarę
ma miarę 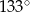 , a kąt
, a kąt 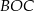 ma miarę
ma miarę 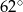 .
.
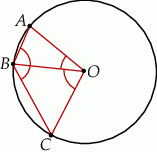
Kąt 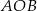 ma miarę
ma miarę
A) 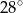 B)
B) 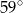 C)
C) 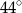 D)
D) 
Dane są punkty 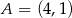 ,
, 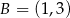 ,
, 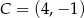 . Pole trójkąta
. Pole trójkąta 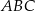 jest równe
jest równe
A) 2 B) 3 C) 6 D) 12
Punkty 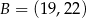 i
i 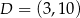 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 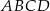 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 20 B) 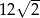 C) 10 D)
C) 10 D) 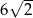
Pole równoległoboku 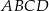 jest równe 120. Na bokach
jest równe 120. Na bokach 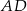 i
i 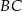 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 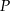 i
i 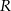 , takie, że
, takie, że 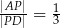 i
i 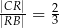 (zobacz rysunek)
(zobacz rysunek)
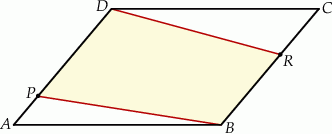
Pole czworokąta 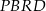 jest równe
jest równe
A) 81 B) 96 C) 102 D) 118
Pole powierzchni całkowitej sześcianu jest równe 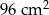 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 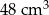 B)
B) 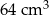 C)
C) 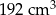 D)
D) 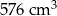
Średnia arytmetyczna wszystkich liczb złożonych należących do przedziału 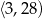 z dokładnością do 0,1 jest równa
z dokładnością do 0,1 jest równa
A) 16,9 B) 17,4 C) 16,3 D) 16,7
W pudełku znajduje się 5 kartek, na których zapisano liczby: 0, 2, 4, 6, 8. Wyjmujemy z pudełka kolejno trzy kartki i układając je jedna obok drugiej tworzymy liczby trzycyfrowe. Liczb takich możemy utworzyć maksymalnie
A) 48 B) 125 C) 100 D) 60
Rzucamy dwiema kostkami do gry. Jeśli 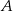 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a 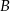 oznacza zdarzenie „suma wyrzuconych oczek jest równa 8” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 8” to
A) 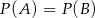 B)
B) 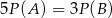 C)
C) 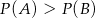 D)
D) 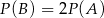
Zadania otwarte
Rozwiąż nierówność 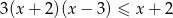 .
.
Rozwiąż równanie 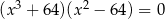 .
.
Przekątne czworokąta 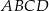 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 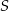 , a punkt
, a punkt 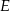 jest takim punktem przekątnej
jest takim punktem przekątnej 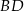 , że
, że 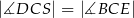 (zobacz rysunek).
(zobacz rysunek).
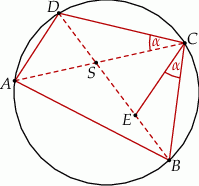
Wykaż, że 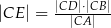 .
.
Rzucamy trzy razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 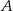 polegającego na tym, że co najmniej jeden raz wypadnie ścianka z dwoma oczkami.
polegającego na tym, że co najmniej jeden raz wypadnie ścianka z dwoma oczkami.
Wykaż, że jeżeli liczby rzeczywiste 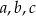 spełniają warunek
spełniają warunek 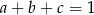 , to
, to
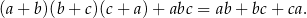
Długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny, w którym największy wyraz jest o 5 większy od wyrazu najmniejszego. Objętość prostopadłościanu jest równa 216. Oblicz długości krawędzi tego prostopadłościanu.
Punkt 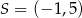 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 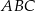 , w którym
, w którym 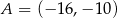 i
i 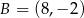 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 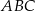 .
.

