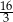Zadanie nr 5480543
Odcinki 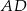 i
i 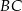 przecinają się w punkcie
przecinają się w punkcie 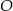 . W trójkątach
. W trójkątach 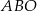 i
i 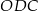 zachodzą związki:
zachodzą związki: 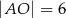 ,
, 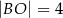 ,
, 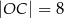 ,
, 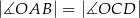 (zobacz rysunek).
(zobacz rysunek).
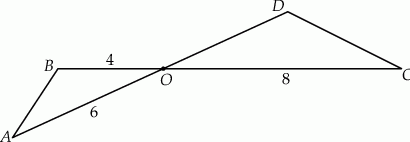
Oblicz długość boku 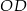 trójkąta
trójkąta 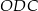 .
.
Rozwiązanie
Zauważmy, że trójkąty 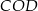 i
i 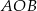 mają dwa równe kąty:
mają dwa równe kąty: 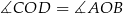 i z założenia
i z założenia 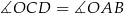 . Są zatem podobne i mamy
. Są zatem podobne i mamy
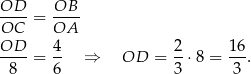
Odpowiedź: