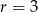Zadanie nr 8273291
Dany jest trójkąt o przyprostokątnych 24 i 7. Wyznacz promień okręgu wpisanego w ten trójkąt.
Rozwiązanie
Zaczynamy od rysunku
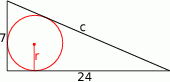
Z twierdzenia Pitagorasa wyznaczamy długość przeciwprostokątnej
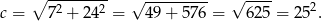
Żeby obliczyć promień okręgu wpisanego skorzystamy z następującego wzoru na pole
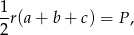
gdzie 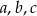 są długościami boków trójkąta. Liczymy pole
są długościami boków trójkąta. Liczymy pole
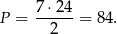
Wyliczamy promień
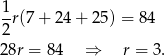
Odpowiedź: