Zadanie nr 8763443
Jedna z przekątnych rombu jest dwa razy dłuższa od drugiej. Wyznacz stosunek obwodu rombu do sumy jego przekątnych.
Rozwiązanie
Zacznijmy od szkicowego rysunku.
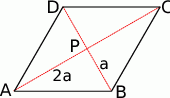
Jeżeli oznaczymy długość krótszej przekątnej przez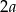 
(
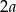, a nie 
, żeby nie mieć ułamków), to druga przekątna ma długość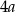 
, zatem z trójkąta prostokątnego 
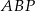(przekątne rombu przecinają się pod kątem prostym) mamy
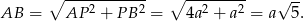
Zatem szukany stosunek wynosi
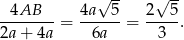
Odpowiedź: 
