Zadanie nr 9252549
Punkty 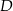 i
i 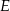 są środkami boków
są środkami boków 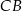 i
i 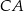 trójkąta
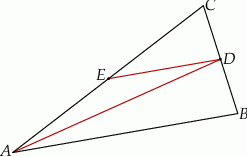
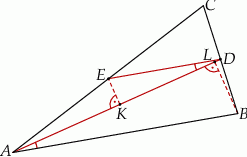
trójkąta 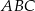 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 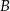 od prostej
od prostej 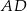 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 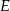 od prostej
od prostej 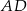 .
.
Rozwiązanie
Dorysujmy rzuty punktów 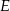 i
i  na tę prostą.
na tę prostą.
Odcinek 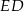 jest odcinkiem łączącym środki boków trójkąta
jest odcinkiem łączącym środki boków trójkąta 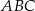 , więc
, więc 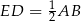 .
.
Sposób I
Zauważmy, że trójkąty prostokątne 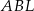 i
i 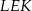 mają równe kąty ostre:
mają równe kąty ostre:
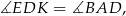
więc są podobne. Ponadto znamy ich skalę podobieństwa 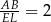 . W takim razie
. W takim razie
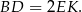
Sposób II
Zauważmy, że wysokość opuszczona na podstawę 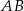 trójkąta
trójkąta 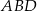 jest taka sama jak wysokość opuszczona na podstawę
jest taka sama jak wysokość opuszczona na podstawę 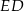 trójkąta
trójkąta 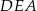 (bo w obu przypadkach jest to odległość między prostymi
(bo w obu przypadkach jest to odległość między prostymi 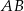 i
i 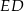 ). Ponadto
). Ponadto 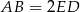 , więc trójkąt
, więc trójkąt 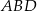 ma dwa razy większe pole niż trójkąt
ma dwa razy większe pole niż trójkąt 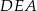 . Stąd
. Stąd