/Szkoła średnia/Geometria/Planimetria

Zadanie nr 9261121

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź długości przekątnych rombu o boku 29 jeżeli wiadomo, że ich różnica długości jest równa 2.

Rozwiązanie

Ponieważ przekątne rombu dzielą się na połowy i są prostopadłe, to trójkąt zaznaczony na rysunku jest trójkątem prostokątnym o przeciwprostokątnej długości 29.

PIC

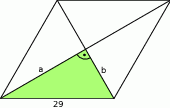
Wiemy ponadto, że

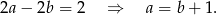
2a − 2b = 2 ⇒ a = b + 1.

Na mocy twierdzenia Pitagorasa, mamy

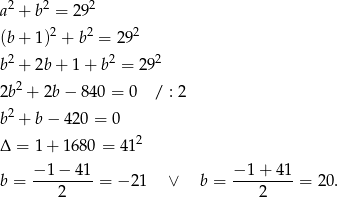
2 2 2 a + b = 29 (b+ 1)2 + b2 = 292 b2 + 2b+ 1+ b2 = 292 2 2b + 2b − 840 = 0 / : 2 b2 + b− 420 = 0 2 Δ = 1+ 1680 = 41 − 1 − 41 − 1+ 41 b = ---------= − 21 ∨ b = ---------= 20 . 2 2

Ujemne rozwiązanie odrzucamy i mamy 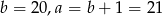b = 20,a = b + 1 = 21 .  
Odpowiedź: 40 i 42

Wersja PDF