Zadanie nr 9336254
Dany jest trójkąt prostokątny 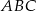 . Na przyprostokątnych
. Na przyprostokątnych 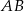 i
i 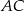 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 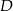 i
i 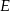 takie, że
takie, że 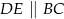 . Na przeciwprostokątnej
. Na przeciwprostokątnej 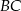 wyznaczono punkt
wyznaczono punkt 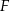 taki, że
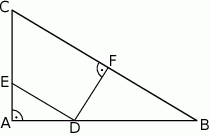
taki, że 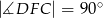 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 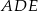 jest podobny do trójkąta
jest podobny do trójkąta 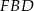 .
.
Rozwiązanie
Zauważmy, że każdy z trójkątów 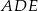 i
i 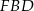 jest prostokątny oraz
jest prostokątny oraz
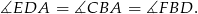
To oznacza, że trójkąty te mają równe kąty, więc są podobne.

