/Szkoła średnia/Geometria/Planimetria

Zadanie nr 9471447

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójkąt 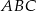ABC , w którym 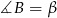∡B = β , a kąt zewnętrzny przy wierzchołku 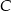C ma miarę α .

PIC

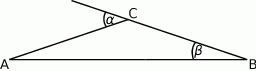
Wykaż, że jeśli 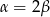α = 2β , to trójkąt 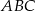ABC jest równoramienny.

Rozwiązanie

Ponieważ kąt zewnętrzny przy wierzchołku 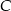C ma miarę α , więc

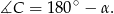
∘ ∡C = 180 − α.

Zatem

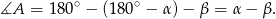
∘ ∘ ∡A = 180 − (180 − α )− β = α − β.

Teraz korzystamy z założenia, że 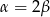α = 2β i otrzymujemy

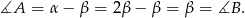
∡A = α − β = 2β− β = β = ∡B .

Zatem trójkąt jest równoramienny.

Wersja PDF