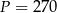/Szkoła średnia/Geometria/Planimetria

Zadanie nr 9503019

Dodaj do ulubionych
Dodaj do rozwiązanych

Przyprostokątne trójkąta prostokątnego 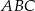ABC mają długości 10 i 24. Przeciwprostokątna trójkąta 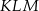KLM podobnego do niego ma długość 39. Oblicz pole trójkąta KLM .

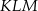Rozwiązanie

Z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej trójkąta 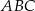ABC

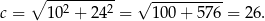
∘ ---------- √ ---------- c = 102 + 242 = 100+ 576 = 2 6.

Obliczamy skalę podobieństwa trójkątów

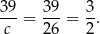
39-= 39-= 3. c 26 2

Teraz możemy łatwo policzyć długości przyprostokątnych trójkąta 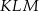KLM

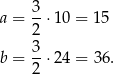
a = 3⋅ 10 = 15 2 3- b = 2 ⋅ 24 = 36.

Jedyne co nam pozostało to policzyć pole powierzchni

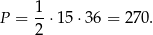
P = 1-⋅15 ⋅36 = 270. 2

 
Odpowiedź: P = 270

Wersja PDF