/Szkoła średnia/Geometria/Planimetria

Zadanie nr 9789916

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane jest koło o promieniu długości 16 cm. W kole tym poprowadzono cięciwę opartą na łuku odpowiadającym kątowi środkowemu o mierze 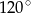120∘ . Znajdź odległość tej cięciwy od środka koła.

Rozwiązanie

Sposób I

Zaczynamy oczywiście od rysunku.

PIC

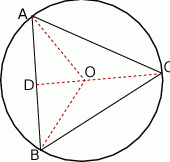
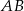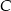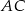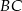Powiedzmy, że dana cięciwa to AB . Jeżeli C jest takim punktem okręgu, że cięciwy AC i BC są oparte na kątach 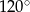120∘ , to trójkąt 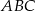ABC jest równoboczny. Szukana odległość to odległość jego środka 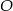O od boku 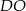DO . Jak wiadomo środek ten dzieli wysokość 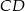CD w stosunku 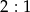2 : 1 . Zatem

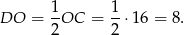
1 1 DO = --OC = -⋅1 6 = 8. 2 2

Sposób II

Tym razem dorysujmy punkt 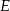E przecięcia się symetralnej odcinka 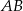AB z okręgiem.

PIC

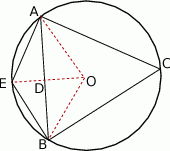
Z własności kątów opisanych na cięciwach

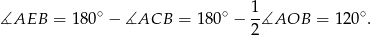
1 ∡AEB = 18 0∘ − ∡ACB = 1 80∘ − -∡AOB = 12 0∘. 2

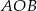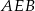Zatem trójkąty AOB i AEB są przystające, czyli czworokąt 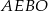AEBO jest rombem. Ponieważ przekątne rombu dzielą się na połowy,

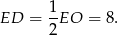
ED = 1EO = 8 . 2

 
Odpowiedź: 8 cm

Wersja PDF