Zadanie nr 9797723
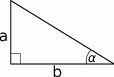
Dany jest trójkąt prostokątny, w którym  ,
, 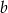 oznaczają długości przyprostokątnych,
oznaczają długości przyprostokątnych,  jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej
jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej  . Wiadomo, że
. Wiadomo, że 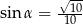 . Oblicz
. Oblicz
- tangens kąta
 ;
; - wartość wyrażenia
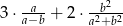 .
.
Rozwiązanie
- Aby obliczyć
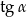 musimy znać
musimy znać 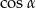 . Ponieważ
. Ponieważ  jest kątem ostrym, mamy
jest kątem ostrym, mamy 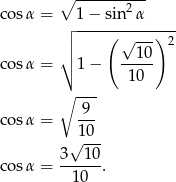
Stąd
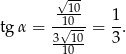
Odpowiedź: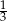
- Z poprzedniego podpunktu wiemy, że
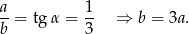
Mamy zatem
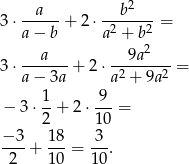
Odpowiedź: