Zadanie nr 1654469

Dla jakich wartości parametru 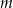równanie 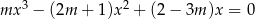3 2 mx − (2m + 1)x + (2− 3m )x = 0 ma rozwiązania, których suma jest dodatnia?

Rozwiązanie

Jedno rozwiązanie podanego równania widać od ręki: 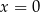x = 0 . Dzieląc przez pozostaje nam równanie kwadratowe

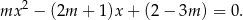
mx 2 − (2m + 1)x + (2 − 3m ) = 0.

Pytanie z treści zadania sprowadza się do pytania kiedy powyższe równanie kwadratowe ma pierwiastki o dodatniej sumie?

Jezeli równanie jest liniowe, czyli 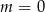m = 0 , to mamy

−x + 2 = 0 ⇒ x = 2

i jest OK.

Jezeli mamy równanie kwadratowe, to sprawdźmy kiedy ma ono pierwiastki

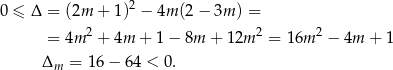
2 0 ≤ Δ = (2m + 1) − 4m (2 − 3m ) = = 4m 2 + 4m + 1 − 8m + 12m 2 = 16m 2 − 4m + 1 Δm = 16 − 64 < 0 .

Równanie ma więc zawsze dwa pierwiastki. Kiedy ich suma jest dodatnia? – na mocy wzorów Viète’a ich suma jest równa

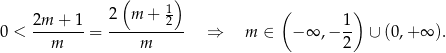
( 1) ( ) 2m + 1 2 m + 2 1 0 < --m---- = -----m----- ⇒ m ∈ −∞ ,− 2- ∪ (0,+ ∞ ).

Odpowiedź: m ∈ (− ∞ ,− 1)∪ ⟨0 ,+∞ ) 2

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz