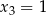Zadanie nr 1832123
Wyznacz wszystkie wartości parametru 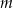 , dla których równanie
, dla których równanie
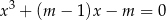
ma dokładnie dwa pierwiastki rzeczywiste. Dla otrzymanych wartości 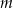 wyznacz te pierwiastki.
wyznacz te pierwiastki.
Rozwiązanie
Jeżeli równanie stopnia 3 ma mieć dwa pierwiastki rzeczywiste, to jeden z nich musi być podwójny.
Sposób I
Lewa strona równania musi mieć postać
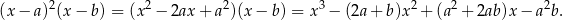
Otrzymujemy stąd układ równań
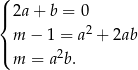
Z pierwszego równania mamy 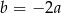 . Podstawiamy tę wartość do dwóch pozostałych równań.
. Podstawiamy tę wartość do dwóch pozostałych równań.
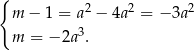
Zauważmy teraz, że jeżeli w drugim równaniu 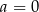 , to
, to 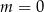 . Ale wtedy z pierwszego równania
. Ale wtedy z pierwszego równania 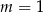 , co jest sprzeczne z tym, że
, co jest sprzeczne z tym, że 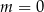 . Zatem
. Zatem 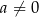 ,
, 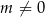 i
i 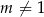 i możemy podzielić stronami drugie równanie przez pierwsze.
i możemy podzielić stronami drugie równanie przez pierwsze.
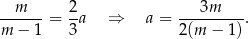
Podstawiamy teraz to wyrażenie np. do drugiego równania.
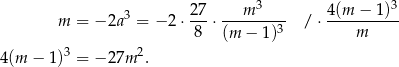
W tym miejscu można dostrzec, że jednym z rozwiązań jest 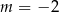 , przyda nam się to za chwilę. Przekształcamy równanie dalej.
, przyda nam się to za chwilę. Przekształcamy równanie dalej.
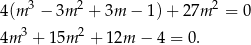
W tym miejscu jesteśmy zmuszeni znaleźć przynajmniej jeden pierwiastek tego równania. Jeżeli nie zauważyliśmy wcześniej, że jednym z pierwiastków jest 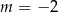 , to znajdujemy go teraz sprawdzając dzielniki wyrazu wolnego. Dzielimy teraz lewą stronę przez
, to znajdujemy go teraz sprawdzając dzielniki wyrazu wolnego. Dzielimy teraz lewą stronę przez 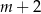 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
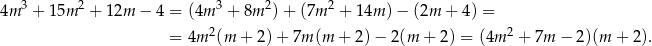
Rozkładamy jeszcze trójmian w nawiasie.
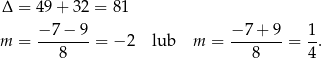
Jeżeli 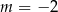 , to
, to 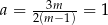 i
i 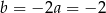 . Jeżeli natomiast
. Jeżeli natomiast 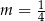 , to
, to
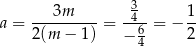
i 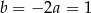 .
.
Sposób II
Tak jak poprzednio zauważamy, że równanie musi mieć jeden pierwiastek podwójny 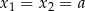 i jeden pojedynczy
i jeden pojedynczy 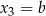 . Korzystamy ze wzorów Viète’a dla równania stopnia 3.
. Korzystamy ze wzorów Viète’a dla równania stopnia 3.
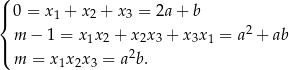
Układ równań rozwiązujemy tak samo jak w poprzednim sposobie.
Sposób III
Korzystamy z prostego do udowodnienia faktu, że pierwiastek podwójny wielomianu jest też pierwiastkiem jego pochodnej. Jeżeli więc  jest pierwiastkiem podwójnym danego równania, to
jest pierwiastkiem podwójnym danego równania, to
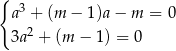
Z drugiego równania mamy
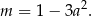
Podstawiamy to wyrażenie do pierwszego równania
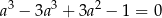
Gołym okiem widać, że jednym z pierwiastków jest 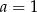 :
:
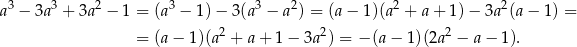
Rozkładamy jeszcze trójmian w nawiasie
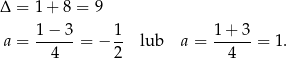
Zatem 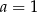 lub
lub 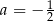 . Mamy wtedy odpowiednio
. Mamy wtedy odpowiednio 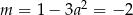 i
i 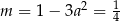 . To jeszcze nie jest całkiem koniec, w każdym z tych przypadków musimy wyznaczyć drugi pierwiastek równania. Jeżeli
. To jeszcze nie jest całkiem koniec, w każdym z tych przypadków musimy wyznaczyć drugi pierwiastek równania. Jeżeli 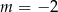 , to
, to
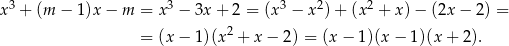
Jeżeli natomiast 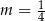 , to
, to
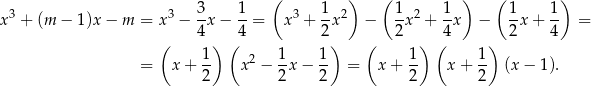
Sposób IV
Zauważmy, że zawsze 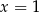 jest pierwiastkiem danego równania, więc możemy podzielić jego lewą stronę przez
jest pierwiastkiem danego równania, więc możemy podzielić jego lewą stronę przez 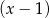 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
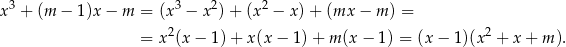
Mamy teraz dwie możliwości: albo wielomian kwadratowy w nawiasie ma dwa pierwiastki i jeden z nich jest równy 1, albo ten wielomian ma jeden pierwiastek różny od 1.
Sprawdźmy najpierw, kiedy 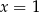 jest pierwiastkiem tego trójmianu
jest pierwiastkiem tego trójmianu
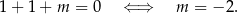
Na mocy wzorów Viète’a drugi pierwiastek 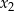 tego równania spełnia
tego równania spełnia
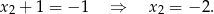
Sprawdźmy teraz drugą możliwość, gdy równanie kwadratowe ma jeden pierwiastek. Tak będzie, gdy
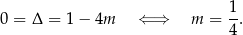
Ten pierwiastek jest wtedy równy
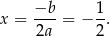
Odpowiedź: 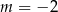 ,
, 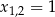 ,
, 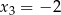 lub
lub 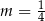 ,
, 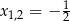 ,
,