/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 2621128

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 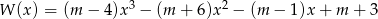3 2 W (x) = (m − 4)x − (m + 6)x − (m − 1)x+ m + 3 jest podzielny przez dwumian 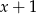x + 1 . Dla jakich wartości parametru 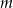m wielomian 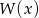W (x) ma dokładnie dwa pierwiastki?

Rozwiązanie

Skoro wielomian 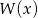W (x) jest podzielny przez dwumian 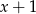x + 1 , to go podzielmy. Zrobimy to grupując wyrazy.

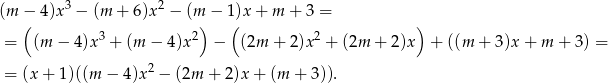
3 2 (m −( 4 )x − (m + 6)x − (m) − 1()x + m + 3 = ) 3 2 2 = (m − 4)x + (m − 4)x − (2m + 2)x + (2m + 2 )x + ((m + 3)x+ m + 3 ) = 2 = (x + 1)((m − 4)x − (2m + 2)x+ (m + 3 )).

Sprawdźmy kiedy wielomian w nawiasie ma dokładnie jeden pierwiastek.

Jeżeli 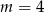m = 4 , to mamy równanie 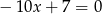− 1 0x+ 7 = 0 , które ma dokładnie jedno rozwiązanie (i jest ono różne od x = − 1 ).

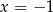Jeżeli 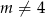m ⁄= 4 , to sprawdźmy kiedy Δ = 0 .

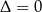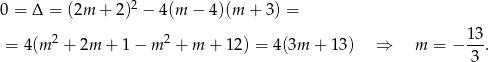
2 0 = Δ = (2m + 2 ) − 4(m − 4)(m + 3) = 2 2 13- = 4(m + 2m + 1 − m + m + 1 2) = 4(3m + 13) ⇒ m = − 3 .

Sprawdźmy jeszcze, kiedy pierwiastkiem badanego równania kwadratowego jest 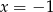x = − 1 (podstawiamy w tym równaniu x = −1 ).

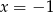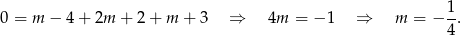
0 = m − 4 + 2m + 2 + m + 3 ⇒ 4m = − 1 ⇒ m = − 1. 4

Liczba 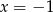x = − 1 jest więc pierwiastkiem trójmianu kwadratowego tylko dla 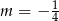m = − 1 4 . W szczególności w przypadku 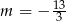m = − 13 3 jedyny pierwiastek równania w nawiasie nie jest równy − 1 .

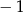Z drugiej strony, jeżeli 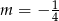1 m = − 4 to patrząc na wyliczoną wcześniej 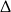Δ -ę, widzimy, że równanie w nawiasie ma dwa pierwiastki i jeden z nich to 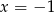x = − 1 . Zatem też w tym przypadku wyjściowe równanie ma dwa pierwiastki.  
Odpowiedź: 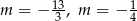13 1 m = − 3 , m = − 4 lub m = 4

Wersja PDF