Zadanie nr 4349484
Udowodnij, że jeżeli wielomian 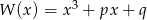 ma trzy pierwiastki, to
ma trzy pierwiastki, to 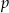 jest liczbą ujemną.
jest liczbą ujemną.
Rozwiązanie
Sposób I
Wiadomo jak wygląda wykres wielomianu stopnia 3. Jeżeli ma on mieć trzy pierwiastki to musi on mieć minimum, które znajduje się poniżej osi 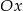 . Sprawdźmy w jakim punkcie jest minimum. Liczymy pochodną
. Sprawdźmy w jakim punkcie jest minimum. Liczymy pochodną
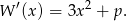
Widać teraz, że aby istniało minimum (czyli, w tej sytuacji, miejsce zerowe pochodnej), 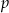 musi być ujemne. Innymi słowy, jeżeli
musi być ujemne. Innymi słowy, jeżeli 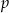 nie jest ujemne, to pochodna jest dodatnia, czyli
nie jest ujemne, to pochodna jest dodatnia, czyli 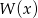 jest funkcją rosnącą i nie może mieć trzech miejsc zerowych.
jest funkcją rosnącą i nie może mieć trzech miejsc zerowych.
Sposób II
Zauważmy, że 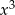 jest funkcją rosnącą, a
jest funkcją rosnącą, a 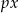 , dla
, dla 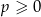 i
i 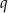 są niemalejące. Zatem dla
są niemalejące. Zatem dla 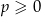 funkcja
funkcja 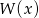 jest funkcją rosnącą i może mieć co najwyżej jedno miejsce zerowe.
jest funkcją rosnącą i może mieć co najwyżej jedno miejsce zerowe.
Na koniec, dla ciekawskich przykładowe wykresy funkcji 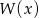 dla
dla 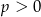 i dla
i dla 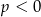 .
.
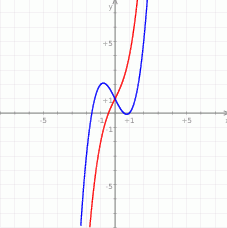
Zauważmy, że tak naprawdę nie ustaliliśmy czy 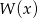 ma trzy pierwiastki dla
ma trzy pierwiastki dla 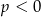 , pokazaliśmy tylko, że jeżeli
, pokazaliśmy tylko, że jeżeli 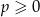 to ma tylko jeden.
to ma tylko jeden.
Sposób III
Na mocy wzorów Viète’a dla wielomianu stopnia 3 mamy
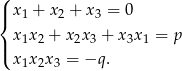
Zatem
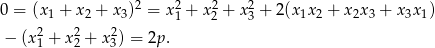
To oczywiście oznacza, że 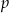 jest liczbą ujemną.
jest liczbą ujemną.

