/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 4556190

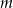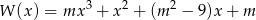Wyznacz wszystkie wartości parametru m , dla których liczba 1 jest jedynym całkowitym pierwiastkiem wielomianu W (x) = mx 3 + x2 + (m 2 − 9)x+ m .

Wersja PDF

Rozwiązanie

Sprawdźmy, kiedy 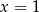x = 1 jest pierwiastkiem wielomianu.

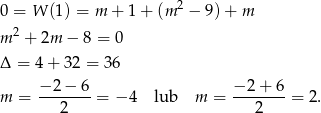
2 0 = W (1) = m + 1+ (m − 9) + m m 2 + 2m − 8 = 0 Δ = 4+ 32 = 36 −-2-−-6 −-2+--6 m = 2 = − 4 lub m = 2 = 2.

Mamy wtedy odpowiednio wielomiany

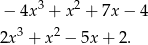
− 4x3 + x2 + 7x − 4 3 2 2x + x − 5x + 2.

Dzielimy teraz każdy z tych wielomianów przez 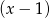(x − 1 ) . My zrobimy to grupując wyrazy.

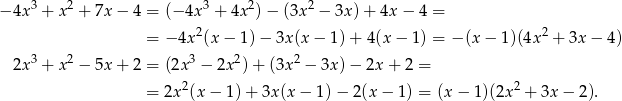
− 4x3 + x2 + 7x − 4 = (− 4x 3 + 4x 2)− (3x2 − 3x) + 4x − 4 = 2 2 = − 4x (x− 1)− 3x(x − 1) + 4(x − 1) = − (x − 1 )(4x + 3x − 4) 2x3 + x2 − 5x + 2 = (2x 3 − 2x2)+ (3x2 − 3x) − 2x + 2 = 2 2 = 2x (x− 1)+ 3x(x − 1) − 2(x − 1) = (x− 1)(2x + 3x − 2).

Liczymy 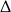Δ –y i pierwiastki trójmianów otrzymanych w nawiasach. Mamy odpowiednio

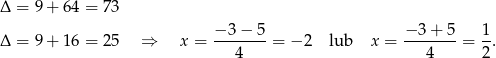
Δ = 9+ 64 = 73 −-3-−-5 −-3-+-5 1- Δ = 9+ 16 = 25 ⇒ x = 4 = − 2 lub x = 4 = 2.

Widać teraz, że w drugim przypadku wyjściowe równanie ma dwa pierwiastki całkowite, a w pierwszym przypadku ma ono tylko jeden pierwiastek wymierny.  
Odpowiedź: m = − 4

Wersja PDF