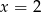/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 5068628

Rozwiąż nierówność 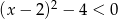2 (x − 2) − 4 < 0 . Podaj wszystkie rozwiązania równania 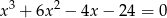x 3 + 6x 2 − 4x− 24 = 0 , które należą do zbioru rozwiązań tej nierówności.

Wersja PDF

Rozwiązanie

Najpierw rozwiązujemy nierówność

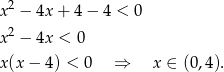
2 x − 4x+ 4− 4 < 0 x2 − 4x < 0 x(x− 4) < 0 ⇒ x ∈ (0,4).

Teraz rozwiązujemy podane równanie. Możemy to zrobić standardowo, czyli szukać pierwiastka całkowitego (łatwo znaleźć 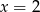x = 2 ) i dzielić przez dwumian. Możemy też od razu dostrzec rozkład

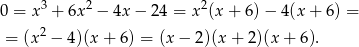
0 = x3 + 6x2 − 4x − 24 = x2(x+ 6)− 4(x + 6) = 2 = (x − 4)(x+ 6) = (x − 2)(x + 2)(x + 6 ).

Spośród otrzymanych pierwiastków tylko 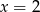x = 2 należy do przedziału (0,4) .  
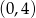Odpowiedź: Nierówność: 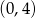(0,4) , równanie: x = 2

Wersja PDF