/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 5085289

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 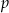p wielomian 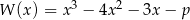3 2 W (x) = x − 4x − 3x − p ma trzy pierwiastki rzeczywiste?

Rozwiązanie

Miejsce umieszczenia parametru we wzorze wielomianu 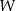W – jako wyrazu wolnego sprawia, że zniknie on, gdy obliczymy pochodną 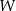W . Liczymy

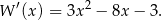
W ′(x) = 3x2 − 8x − 3 .

Rozkładamy teraz ten trójmian

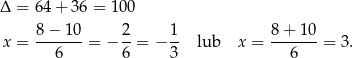
Δ = 6 4+ 3 6 = 100 8− 10 2 1 8 + 10 x = -------= − --= − -- lub x = -------= 3. 6 6 3 6

Stąd

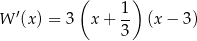
( 1) W ′(x) = 3 x+ -- (x− 3) 3

i wielomian 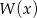W (x) ma dwa ekstrema lokalne – maksimum w punkcie 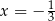1 x = − 3 i minimum w punkcie 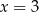x = 3 . Obliczmy jeszcze wartości funkcji 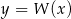y = W (x) w tych punktach.

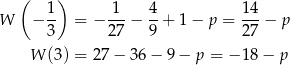
( ) 1- -1- 4- 14- W − 3 = − 27 − 9 + 1− p = 27 − p W (3 ) = 27 − 36 − 9 − p = − 18 − p

Możemy teraz naszkicować wykres tej funkcji.

PIC

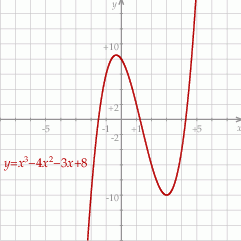
Z wykresu widać, że dane równanie ma trzy pierwiastki rzeczywiste wtedy i tylko wtedy, gdy

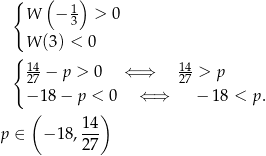
{ ( ) W − 1 > 0 3 W (3) < 0 { 14 14 27 − p > 0 ⇐ ⇒ 27 > p − 18 − p < 0 ⇐ ⇒ − 18 < p. ( ) p ∈ − 18 , 14 27

 
Odpowiedź: ( ) p ∈ − 18, 14 27

Wersja PDF