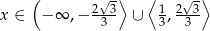/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 5420937

Dany jest wielomian 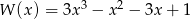3 2 W (x) = 3x − x − 3x + 1 .

  • Rozłóż wielomian na czynniki liniowe.
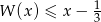  • Rozwiąż nierówność W (x) ≤ x − 1 3 .
Wersja PDF

Rozwiązanie

  • Możemy wielomian rozłożyć szukając pierwiastków i dzieląc przez dwumiany, ale można też to zrobić wprost.
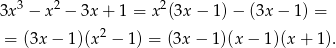
    3x3 − x2 − 3x + 1 = x 2(3x − 1)− (3x− 1) = 2 = (3x − 1)(x − 1) = (3x − 1)(x− 1)(x + 1).

     
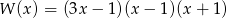
    Odpowiedź: W (x ) = (3x− 1)(x − 1)(x + 1)

  • Liczymy
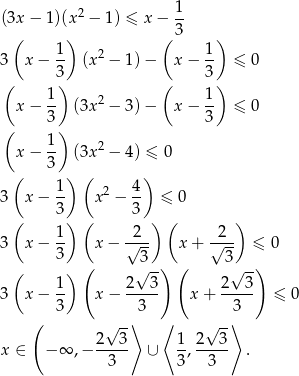
    1 (3x − 1)(x 2 − 1 ) ≤ x− -- ( ) ( 3 ) 3 x − 1- (x2 − 1) − x − 1- ≤ 0 3 3 ( 1) ( 1) x − -- (3x2 − 3) − x − -- ≤ 0 ( 3) 3 1 2 x − -- (3x − 4) ≤ 0 ( 3 ) ( ) 1- 2 4- 3 x − 3 x − 3 ≤ 0 ( ) ( ) ( ) 3 x − 1- x − √2-- x + √2-- ≤ 0 3 3 3 ( ) ( √ -) ( √ --) 3 x − 1- x − 2---3 x + 2--3- ≤ 0 3 3 3 ( √ --⟩ ⟨ √ -⟩ 2--3- 1- 2--3- x ∈ − ∞ ,− 3 ∪ 3 , 3 .

     
    Odpowiedź: ( √ -⟩ ⟨ √-⟩ x ∈ −∞ ,− 233- ∪ 13, 233

Wersja PDF