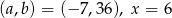/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 5471140

Dodaj do ulubionych
Dodaj do rozwiązanych

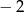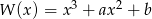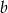Liczby − 2 i 3 są pierwiastkami wielomianu 3 2 W (x) = x + ax + b . Wyznacz liczby a i b oraz trzeci pierwiastek wielomianu.

Rozwiązanie

Podstawiając podane pierwiastki do wzoru wielomianu otrzymujemy układ równań

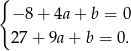
{ − 8+ 4a+ b = 0 27+ 9a+ b = 0.

Odejmujemy od drugiego równania pierwsze (żeby skrócić 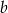b ) i mamy

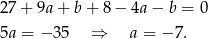
27+ 9a + b+ 8− 4a− b = 0 5a = − 35 ⇒ a = − 7.

Z pierwszego równania mamy więc 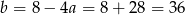b = 8− 4a = 8 + 28 = 36 . Mamy więc do czynienia z wielomianem

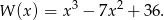
W (x) = x 3 − 7x 2 + 3 6.

Wiemy, że wielomian ten jest podzielny przez

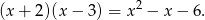
(x + 2)(x − 3) = x 2 − x − 6 .

Wykonujemy to dzielnie – my zrobimy to grupując wyrazy.

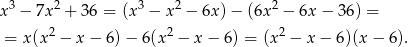
3 2 3 2 2 x − 7x + 36 = (x − x − 6x) − (6x − 6x − 36) = = x(x 2 − x − 6)− 6 (x2 − x− 6) = (x2 − x − 6)(x − 6).

Trzecim pierwiastkiem wielomianu jest więc 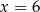x = 6 .  
Odpowiedź: (a,b) = (− 7 ,36), x = 6

Wersja PDF