/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 6818039

Dodaj do ulubionych
Dodaj do rozwiązanych

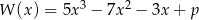Liczba 2 5 jest pierwiastkiem wielomianu 3 2 W (x) = 5x − 7x − 3x + p . Wyznacz pozostałe pierwiastki tego wielomianu i rozwiąż nierówność W (x) > 0 .

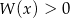Rozwiązanie

Wyznaczamy najpierw parametr 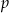p

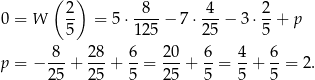
( 2 ) 8 4 2 0 = W -- = 5⋅ ----− 7 ⋅---− 3 ⋅--+ p 5 125 25 5 8-- 2-8 6- 20- 6- 4- 6- p = − 25 + 2 5 + 5 = 25 + 5 = 5 + 5 = 2.

Zatem

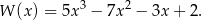
W (x ) = 5x3 − 7x2 − 3x + 2.

Wiemy, że jednym z pierwiastków tego wielomianu jest 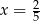x = 2 5 , więc dzielimy go przez 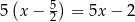( 5) 5 x − 2 = 5x − 2 . My zrobimy to grupując wyrazy.

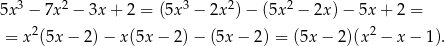
3 2 3 2 2 5x − 7x − 3x+ 2 = (5x − 2x )− (5x − 2x)− 5x + 2 = = x 2(5x− 2)− x(5x − 2) − (5x − 2) = (5x− 2)(x2 − x − 1).

Rozkładamy teraz trójmian w nawiasie.

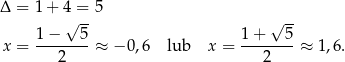
Δ = 1 + 4 = 5 1 − √ 5- 1 + √ 5- x = --------≈ − 0,6 lub x = --------≈ 1,6. 2 2

Pozostało rozwiązać nierówność

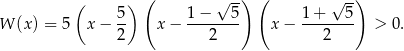
( ) ( ) ( 5 ) 1 − √ 5- 1+ √ 5- W (x ) = 5 x − -- x− -------- x − -------- > 0. 2 2 2

Szkicujemy wielomian stopnia 3.

PIC

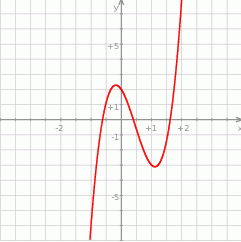
Z wykresu odczytujemy rozwiązanie nierówności

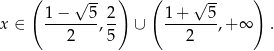
( √ -- ) ( √ -- ) 1-−---5- 2- 1+----5- x ∈ 2 ,5 ∪ 2 ,+ ∞ .

 
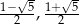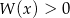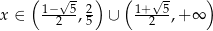Odpowiedź: Pierwiastki: 1−√ 5 1+√ 5 --2--,--2-- , W (x) > 0 dla ( √- ) ( √ - ) x ∈ 1−--5, 2 ∪ 1+--5,+ ∞ 2 5 2 .

Wersja PDF