Zadanie nr 6854996
Wielomian 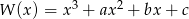 ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy
ma trzy pierwiastki rzeczywiste, które tworzą ciąg arytmetyczny o różnicy 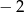 . Oblicz współczynniki
. Oblicz współczynniki 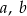 i
i  wiedząc, że
wiedząc, że 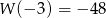 .
.
Rozwiązanie
Pierwiastki wielomianu mogą być zapisane w postaci: 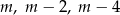 . Mamy zatem równość
. Mamy zatem równość
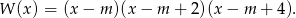
Warunek 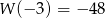 jest więc równoważny równości
jest więc równoważny równości
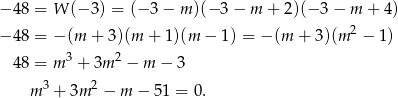
Szukamy teraz miejsc zerowych powyższego wielomianu – sprawdzamy najpierw dzielniki wyrazu wolnego, czyli liczby 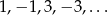 . Gdy to zrobimy okaże się, że jednym z miejsc zerowych jest
. Gdy to zrobimy okaże się, że jednym z miejsc zerowych jest 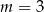 . Dzielimy teraz ten wielomian przez
. Dzielimy teraz ten wielomian przez 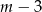 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
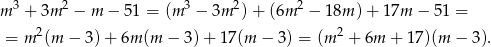
Trójmian w nawiasie nie ma pierwiastków rzeczywistych (bo 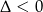 ), więc jedynym rozwiązaniem jest
), więc jedynym rozwiązaniem jest 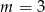 . Mamy wtedy
. Mamy wtedy
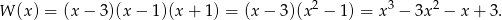
Odpowiedź: