/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 7651168

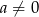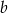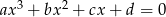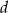Dane są liczby wymierne a ⁄= 0 i b takie, że równanie 3 2 ax + bx + cx+ d = 0 ma dwa pierwiastki wymierne. Wykaż, że c i d są liczbami wymiernymi.

Wersja PDF

Rozwiązanie

Sposób I

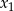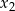Skoro dane równanie ma dwa pierwiastki wymierne x 1 i x2 to wielomian po lewej stronie równania musi mieć rozkład postaci

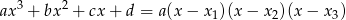
ax 3 + bx 2 + cx + d = a(x − x1)(x − x 2)(x − x 3)

dla pewnej liczby rzeczywistej 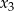x3 . Zauważmy, że po wymnożeniu nawiasów z prawej strony otrzymamy wielomian, którego współczynnik przy 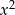x2 jest równy

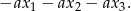
−ax 1 − ax2 − ax3.

Z drugiej strony (patrząc na lewą stronę tej równości) jest on równy 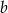b , co daje równanie

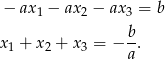
− ax − ax − ax = b 1 2 3 b- x1 + x2 + x3 = − a .

Powyższa równość oznacza, że 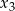x3 jest również liczbą wymierną. To z kolei oznacza, że wielomian

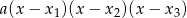
a(x − x1)(x − x 2)(x− x3)

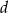ma wszystkie współczynniki wymierne, czyli c i d są liczbami wymiernymi.

Sposób II

Wielomian stopnia 3 ma zawsze 1 lub 3 pierwiastki rzeczywiste (licząc z krotnościami), więc dane równanie musi mieć 3 pierwiastki 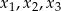x1,x2,x 3 . Możemy więc zastosować wzory Viète’a dla równania stopnia 3.

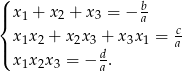
( | x 1 + x 2 + x 3 = − b { a -c | x 1x2 + x2x3 + x3x1 = a ( x 1x2x3 = − d. a

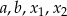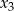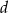Jeżeli teraz założymy, że a,b,x ,x 1 2 są liczbami wymiernymi, to z pierwszego z tych wzorów wynika, że x3 też jest liczbą wymierną. Wtedy jednak, na mocy dwóch pozostałych wzorów, c i d też są liczbami wymiernymi.

Wersja PDF