/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 8529863

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 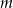m , dla których równanie

2 2 (x− 3)[x − 2(2m + 1 )x+ (m + 2) ] = 0

ma trzy różne rozwiązania.

Rozwiązanie

Podane równanie ma na pewno jeden pierwiastek 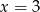x = 3 . Jeżeli równanie ma mieć trzy pierwiastki, to trójmian w nawiasie musi mieć dwa pierwiastki i żaden z nich nie może być równy 3. Na początek liczymy 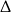Δ -ę.

[ ] 0 < Δ = 4(2m + 1)2 − 4(m + 2)2 = 4 (2m + 1 )2 − (m + 2)2 / : 4 0 < (2m + 1 − (m + 2))((2m + 1)+ (m + 2)) = (m − 1)(3m + 3) / : 3 0 < (m − 1)(m + 1) ⇒ m ∈ (− ∞ ,− 1)∪ (1,+ ∞ ).

To jeszcze nie koniec, bo musimy mieć pewność, że żaden z pierwiastków równania kwadratowego nie jest równy 3. Sprawdźmy kiedy tak jest

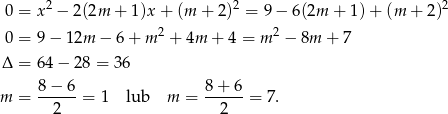
0 = x 2 − 2(2m + 1)x + (m + 2)2 = 9 − 6(2m + 1) + (m + 2)2 2 2 0 = 9 − 12m − 6 + m + 4m + 4 = m − 8m + 7 Δ = 64 − 28 = 36 m = 8-−-6-= 1 lub m = 8-+-6-= 7. 2 2

Te wartości 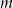m musimy usunąć ze zbioru rozwiązań, więc ostatecznie

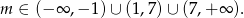
m ∈ (− ∞ ,− 1)∪ (1 ,7 )∪ (7,+ ∞ ).

 
Odpowiedź: m ∈ (− ∞ ,− 1)∪ (1,7) ∪ (7,+ ∞ )

Wersja PDF