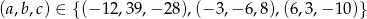Zadanie nr 8938210
Suma wszystkich czterech współczynników wielomianu 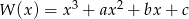 jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 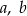 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Rozwiązanie
Wiemy, że
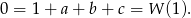
Sposób I
Pierwiastki wielomianu mogą być zapisane w postaci: 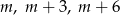 . Mamy zatem równość
. Mamy zatem równość
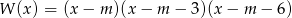
Warunek 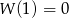 jest więc równoważny równości
jest więc równoważny równości
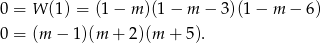
Mamy zatem trzy ciągi spełniające warunki zadania.
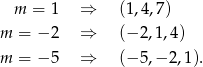
Pozostało obliczyć w każdym z powyższych przypadków współczynniki wielomianu.
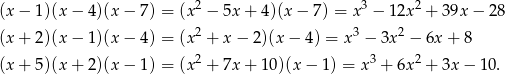
Sposób II
Wiemy, że 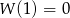 , czyli jedynym z pierwiastków wielomianu jest
, czyli jedynym z pierwiastków wielomianu jest 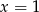 . Ponieważ pierwiastki wielomianu tworzą ciąg arytmetyczny o różnicy 3, to mamy trzy możliwe konfiguracje pierwiastków
. Ponieważ pierwiastki wielomianu tworzą ciąg arytmetyczny o różnicy 3, to mamy trzy możliwe konfiguracje pierwiastków
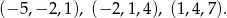
Pozostało obliczyć w każdym z powyższych przypadków współczynniki wielomianu.
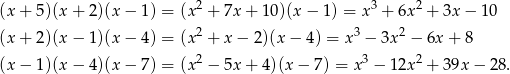
Odpowiedź: