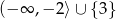Zadanie nr 9012777
Wielomian 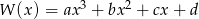 , gdzie
, gdzie 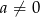 , ma dwa różne miejsca zerowe:
, ma dwa różne miejsca zerowe: 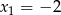 oraz
oraz 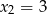 , przy czym pierwiastek
, przy czym pierwiastek 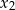 jest dwukrotny. Dla argumentu 1 wartość wielomianu jest równa
jest dwukrotny. Dla argumentu 1 wartość wielomianu jest równa 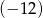 .
.
- Wyznacz wartości współczynników
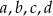 .
. - Dla wyznaczonych współczynników rozwiąż nierówność
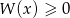 .
.
Rozwiązanie
Z podanych miejsc zerowych wiemy, że wielomian musi mieć postać
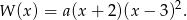
Współczynnik  wyznaczamy korzystając z podanej wartości
wyznaczamy korzystając z podanej wartości 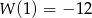 .
.
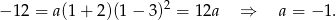
Zatem
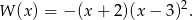
- Współczynniki
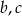 i
i 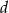 wyznaczymy wymnażając prawą stronę otrzymanego wzoru na
wyznaczymy wymnażając prawą stronę otrzymanego wzoru na 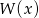 .
. 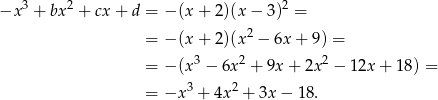
Zatem
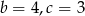 i
i 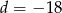 .
.
Odpowiedź: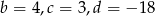
- Musimy rozwiązać nierówność
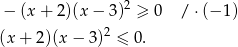
Jeżeli
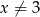 to drugi składnik jest dodatni i pozostaje nierówność
to drugi składnik jest dodatni i pozostaje nierówność 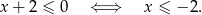
Z drugiej strony, dla
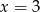 nierówność jest spełniona, co daje nam zbiór rozwiązań
nierówność jest spełniona, co daje nam zbiór rozwiązań 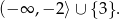
Odpowiedź: