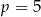Zadanie nr 9122359
Dany jest wielomian 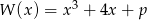 , gdzie
, gdzie 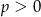 jest liczbą pierwszą. Znajdź
jest liczbą pierwszą. Znajdź 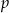 wiedząc, że
wiedząc, że 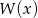 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Rozwiązanie
Jeżeli podany wielomian ma mieć pierwiastek całkowity, to musi to być dzielnik wyrazu wolnego, czyli jedna z liczb 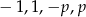 . Dla
. Dla 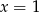 lub
lub 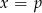 mamy
mamy 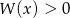 , pozostaje więc sprawdzić co się dzieje dla
, pozostaje więc sprawdzić co się dzieje dla 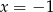 i
i 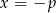 . Dla
. Dla 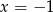 mamy
mamy
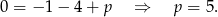
Dla 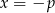 mamy
mamy
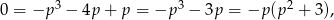
co nie jest możliwe.
Odpowiedź: