/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 9301794

Dodaj do ulubionych
Dodaj do rozwiązanych

Wiedząc, że liczba 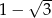√ -- 1 − 3 jest pierwiastkiem wielomianu 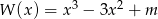3 2 W (x) = x − 3x + m , wyznacz wartość parametru m .

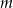Rozwiązanie

Wstawiamy podaną liczbę do wzoru na 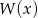W (x ) i przyrównujemy do 0. Po drodze będziemy korzystać ze wzorów skróconego mnożenia

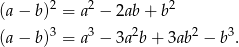
2 2 2 (a− b ) = a − 2ab+ b (a− b )3 = a3 − 3a2b+ 3ab2 − b3.

Liczymy

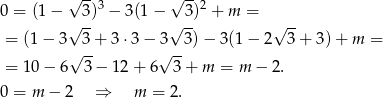
0 = (1 − √ 3)3 − 3(1 − √ 3)2 + m = √ -- √ -- √ -- = (1− 3 3 + 3 ⋅3− 3 3)− 3(1− 2 3 + 3)+ m = √ -- √ -- = 10 − 6 3 − 12 + 6 3 + m = m − 2. 0 = m − 2 ⇒ m = 2.

 
Odpowiedź: m = 2

Wersja PDF