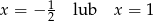/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 9419669

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 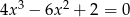3 2 4x − 6x + 2 = 0 .

Rozwiązanie

Sposób I

Liczymy

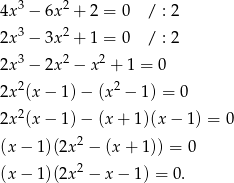
3 2 4x − 6x + 2 = 0 / : 2 2x3 − 3x 2 + 1 = 0 / : 2 2x3 − 2x 2 − x 2 + 1 = 0 2 2 2x (x − 1 )− (x − 1) = 0 2x2(x − 1 )− (x + 1)(x − 1) = 0 2 (x − 1)(2x − (x + 1)) = 0 (x − 1)(2x 2 − x − 1) = 0.

Liczymy wyróżnik trójmianu i pierwiastki

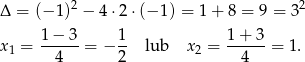
Δ = (− 1)2 − 4⋅2 ⋅(− 1) = 1 + 8 = 9 = 32 1−--3- 1- 1-+-3- x1 = 4 = − 2 lub x 2 = 4 = 1.

Zatem ostatecznie otrzymujemy równanie

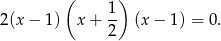
( ) 2(x − 1) x + 1- (x − 1) = 0 . 2

Zatem rozwiązaniami są liczby 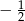− 1 2 i 1.

Sposób II

Jak poprzednio zapisujemy równanie w postaci

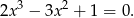
2x3 − 3x2 + 1 = 0 .

Szukamy teraz pierwiastków wśród dzielników wyrazu wolnego. Łatwo zauważyć, że pierwiastkiem jest 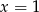x = 1 . Dzielimy teraz wielomian przez 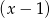(x − 1) – my zrobimy to grupując wyrazy.

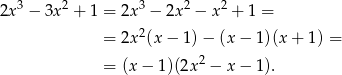
2x3 − 3x2 + 1 = 2x 3 − 2x 2 − x 2 + 1 = = 2x 2(x− 1)− (x − 1)(x+ 1) = 2 = (x − 1)(2x − x − 1).

Dalej postępujemy dokładnie tak samo jak w poprzednim sposobie,  
Odpowiedź: 1 x = − 2 lub x = 1

Wersja PDF