/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 9453569

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla dowolnej wartości parametru a równanie

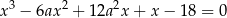
3 2 2 x − 6ax + 12a x + x − 18 = 0

ma dokładnie jedno rozwiązanie rzeczywiste.

Rozwiązanie

Jeżeli oznaczymy wielomian z lewej strony równania przez 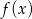f(x) , to

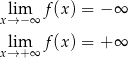
lim f (x ) = − ∞ x→ −∞ lim f (x ) = + ∞ x→ +∞

(bo jest to wielomian stopnia 3). To oznacza, że równanie zawsze ma co najmniej jedno rozwiązanie. Liczymy teraz pochodną

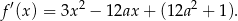
f′(x ) = 3x2 − 12ax + (12a2 + 1).

Ponadto

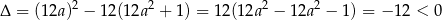
Δ = (12a )2 − 1 2(12a2 + 1) = 12(12a 2 − 1 2a2 − 1) = − 12 < 0

To oznacza, że pochodna jest zawsze dodatnia, czyli funkcja 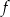f jest rosnąca na całej swojej dziedzinie 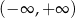(− ∞ ,+ ∞ ) . Zatem wartość 0 może przyjmować tylko w jednym punkcie.

Wersja PDF